Variational Autoencoder
这篇文章来介绍一个经典的生成模型,Variational Auto Encoder,也被称为VAE。它有着比较好的效果和比较优美的理论推导,也是理解最近大放异彩的模型diffusion model的基础。
Auto-Encoder
介绍VAE之前,首先来了解一下什么是Auto-Encoder。Auto-Encoder的结构非常简单,就是将一个目标编码到更低维的空间,然后再解码回原有空间的过程。编码过程被称为encode,解码过程被称为decode,被广泛应用于数据压缩等,而物体编码后一般得到的是一个向量,被称为embedding vector,编码后的空间被称为embedding space,或者说latent space。
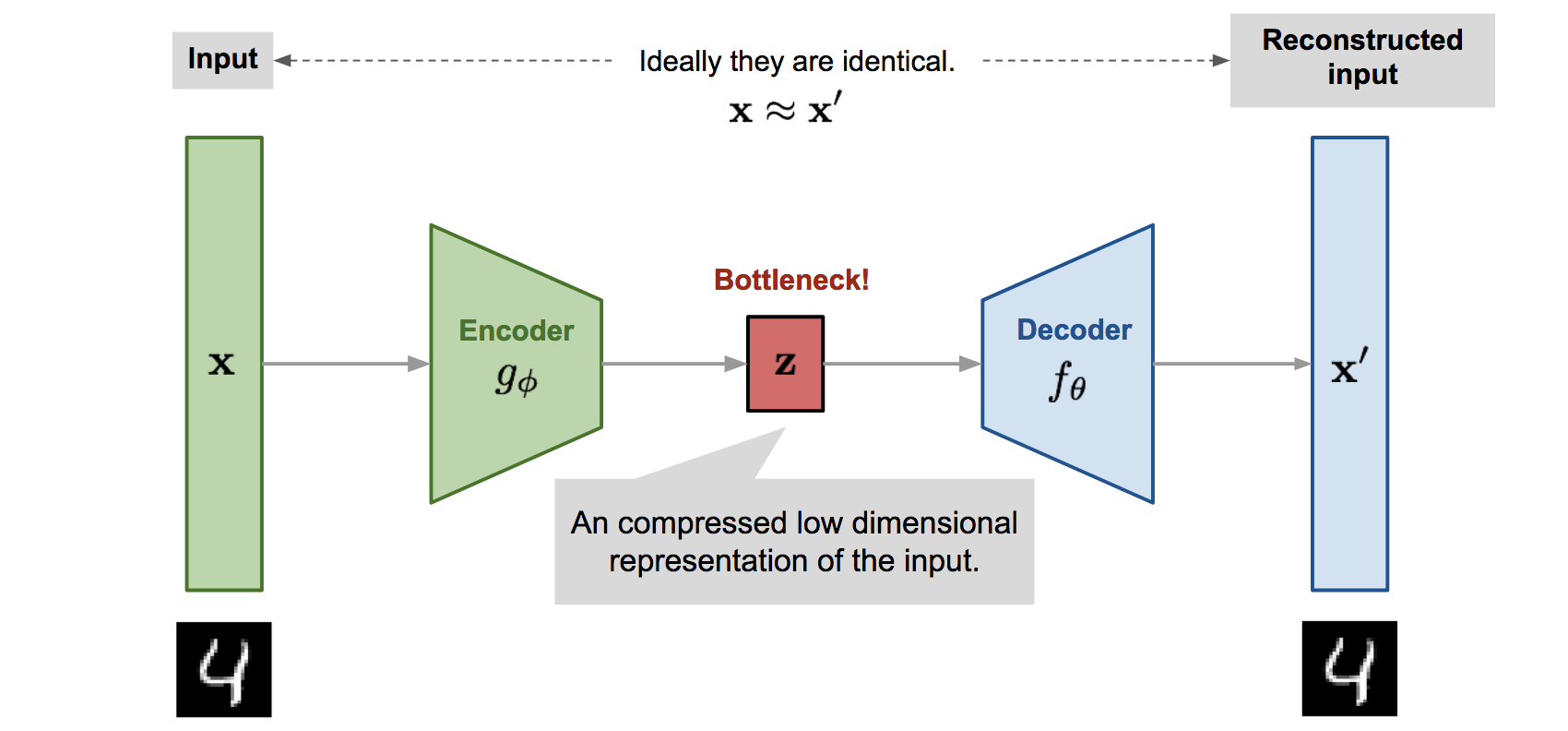
上图中,输入被标记为\(x\),重建后的结果被标记为\(x’\),而latent embedding被标记为\(z\)。而训练auto encoder的loss function也是可以有多种选择的,只要能衡量\(x\)与\(x’\)之间的距离就可以,比如最简单的MSE,或者对于二进制的图像也可以用BCE。
Auto Encoder一般对于训练集中的图像编码重建效果是很好的,但是它的生成效果却不太行。这是因为Auto Encoder的编码其实是一对一地训练出来的,很容易overfitting,对于处于二者”中间“的物体就没有被考虑到。它仿佛就是考虑”是“或者”不是“两个问题,而不会考虑到物体之间的”相似距离“。如果我们对Auto Encoder的embedding space进行采样或者插值,得到的结果就比较差了。
Variational Auto-Encoder
VAE的诞生被用来很好地去解决AE的缺点。VAE的架构和AE的架构非常像。它的想法很简单:既然Auto-Encoder是一个one-to-one的编码过程,所以有了上面的问题,那么是不是可以将对象不要进行这样严格的一对一映射,而是将其映射到一个分布上。而知道一个embedding vector在不同的分布下被sample出的概率,就可以得到其与不同的物体之间的”相似性“。因此这样的方法应该能更好的面对没有见过的样本,也应该有更好的生成效果。
以上的这些其实只是一个intuition,并不是很严格的表达。下面我们来看一下VAE的架构图,已经它应该被怎样去训练(Loss function)。
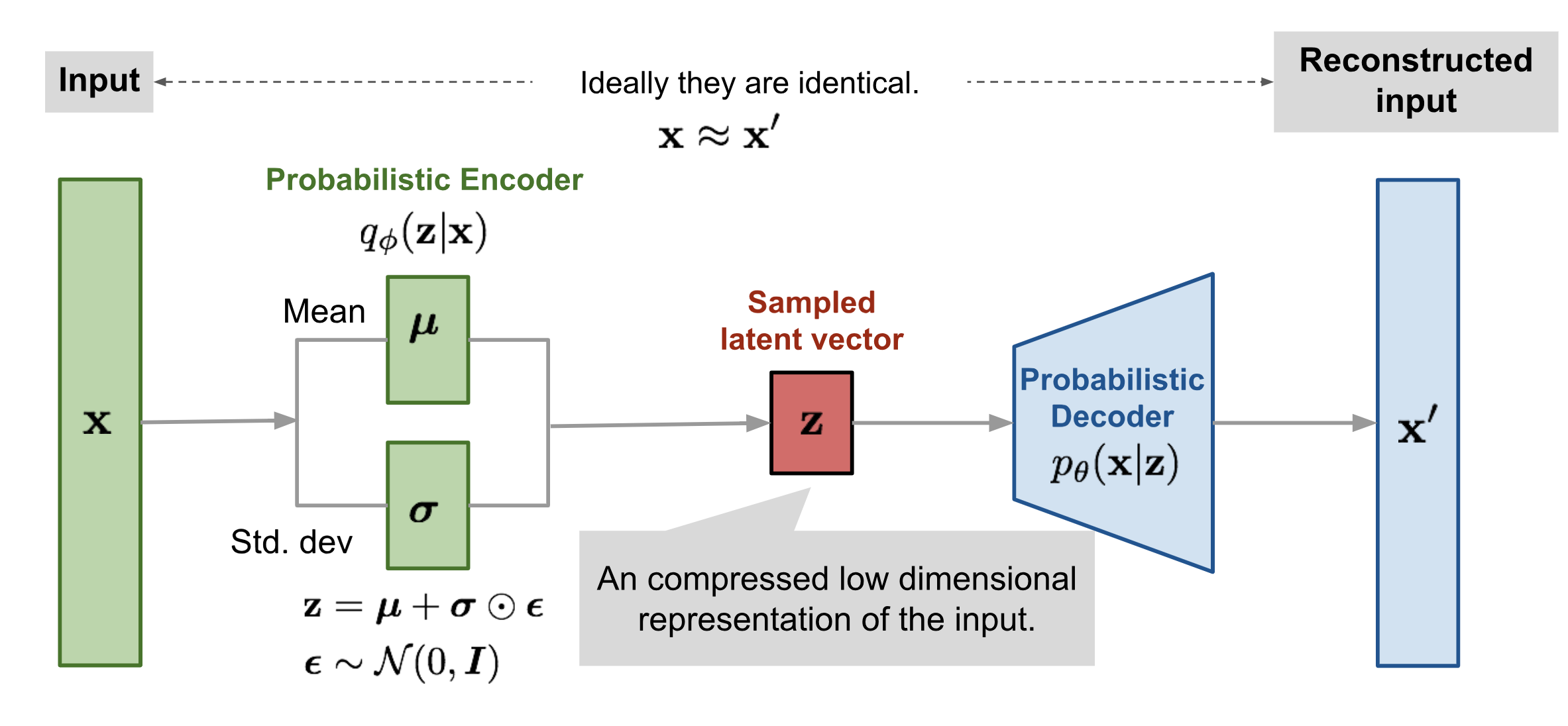
Lower bound推导
当有两个分布\(P_\theta\)与\(P_{\text{data}}\),且有一堆sample:\(x_1, x_2,…,x_n ~ P_{\text{data}}\),那么如果我们想要让\(P_{}\)
我们假设根据我们的网络参数\(\theta\)所生成的数据的分布为\(P_\theta\),那么我们当然希望的是生成这些已知sample的概率是最大的,也就是:
\[ \theta^* = {\arg\max}_{\theta}\prod p_\theta(x) = {\arg\max}_{\theta}\prod \log p_\theta(x). \]
但是 \(p_\theta(x)\)是什么样子我们不知道,因为它并不是简单的正态分布这样的,有一个很明确的数学表达式。但是我们可以通过下面的方式去计算它:
\[ \begin{aligned}\log p_{\theta}(x) &= \log p_\theta(x) \cdot \int _zq(z|x)d_z\\&= \int_z \log p_\theta(x) \cdot q(z|x)d_z\\ &= \int_z q(z|x) \log \frac{p(x, z)}{p(z|x)} d_z \\ &= \int_z q(z|x)\log\frac{q(z|x)p(x,z)}{p(z|x)q(z|x)}d_z \\ &=\int_zq(z|x)\log\frac{q(z|x)}{p(z|x)}d_z + \int_z q(z|x)\log \frac{p(x,z)}{q(z|x)}d_z \\ &= D_\text{kl}\left(q(z|x) \Vert p(z|x)\right) + \int_z q(z|x)\log \frac{p(x,z)}{q(z|x)}d_z \\ &\geq \int_z q(z|x)\log \frac{p(x,z)}{q(z|x)}d_z \\&= \int_z q(z|x)\log \frac{p(z) p(x|z)}{q(z|x)}d_z \\ &= \int_z q(z|x)\log \frac{p(z)}{q(z|x)}d_z + \int_z q(z|x)\log p(x|z)d_z\\ &= - D_\text{KL}\left(q(z|x)\Vert p(z)\right) + \mathbb E_{q(z|x)}\left[\log p(x|z)\right]\end{aligned} \]
上述推导中,\(\theta\)部分被省略。最后得到的结果实际上是一个下界(lower bound)。我们可以通过最大化其lower bound从而最大化我们想要的目标。首先我们要知道,\(q(z|x)\)可以是任何分布,自然也可以是我们的encoder得到的分布。而\(P(z)\)我们希望它是一个标准的正态分布,因此式中的第一项告诉我们,如果想要最大化我们的目标,实际上是需要最小化每一个sample输入到编码器以后得到的分布与标准整体分布之间的KL divergence。而第二项呢,其实是想要最大化在\(q(z|x)\)的分布下,计算条件概率\(\log p(x|z)\)的期望值。直观来说就是如何让\(p(x|z)\)最大,那么自然就是让解码器能尽可能从\(z\)恢复出给定的\(x\),因此第二项实际上可以用reconstruction loss来代替(这样的说法可能并不严格)。
最终VAE的loss是由一个KL divergence与一个reconstruction loss相加得到的。
Reparameterization
在计算loss的时候,要计算reconstruction loss,我们就需要从\(q(z|x)\)中sample一个z出来。如果我们直接sample,这个过程是无法求导的。因此我们可以通过reparameterization技巧来计算,背后的原理就是任何一个高斯分布都可以用一个标准正太分布去表示,因此对于原有分布的采样\(z\)可以进一步表示为:
\[ z = \mu + \sigma \cdot \epsilon, \epsilon \sim N(0, 1) . \]
另外,对两个高斯分布\(\mathcal N(\mu_1, \sigma_1^2), \mathcal N(\mu_2, \sigma_2^2)\)之间的KL divergence,我们也可以通过下式去计算: \[ D_{\textbf{KL}}\left(\mathcal N(\mu_1, \sigma_1^2)\Vert \mathcal N(\mu_2, \sigma_2^2)\right) = \log \frac{\sigma_2}{\sigma_1} + \frac{\sigma_1^2 +(\mu_1 - \mu_2)^2}{2 \sigma_2^2} - \frac{1}{2} \] 所以最终的loss 就变得很简单了。
Log-Variance
在具体的实现中,我们经常会发现神经网络去拟合的并不直接是\(\sigma\)或者\(\sigma^2\),而是叫做logvar
,也就是\(\log \sigma^2 =
2\log\sigma\),这样其实是为了方便计算,因为\(\sigma^2\)总是大于零的,但是网络的拟合并不能总是保证这一点。通过加上一个对数,就能使得其范围拓展到负数了。相应的loss也会根据其进行调整。