图形学——计算机动画
计算机图形学中比较重要的一个应用就是动画。除了用于电影,游戏等制作,动画在军事模拟,实景演示也有非常重要的地位。这一篇文章将简单说一下计算机图形学中动画的发展还有一些算法。
实际上,我们对于二维动画的原理都非常清楚,也就是由一系列帧组成,这也是视频的原理。现在技术的发展极大方便了动画电影的制作,而很久之前动画的每一帧可能都是大师亲手画出来的,因此那时候的动画电影,什么大闹天宫之类的,放到现在都是非常珍贵的遗产。而前几年也有一部即使在现代社会,依然是用画师手绘的电影,叫《挚爱梵高》。手绘的动画这么难能可贵,正是因为计算机动画技术的发展。
对于动画,当然一样是一个大话题,这篇文章会尽量找到提到的算法的paper,想要详细了解需要阅读paper原文。
二维动画
图像变形(Image Morphing)
二维的图像变形实际上我们在西游记中已经见过很多次,妖怪现形,比如从人脸变成了一张豹子脸,这就是一种图像变形。图像变形有两种方法:一种是基于单张图像进行变形,另外是基于多张图像,通过做插值计算进行变形。第一种就不多说了,我们主要讲第二种。
二维图像变形的问题描述为:对于任意给定两幅不带任何几何信息的图像S(source)和D(destination),如何将S很自然地变形为D?主要有以下几个核心问题:
- 如何找到图像S和D各个像素之间的对应关系?
- 对于彩色图像,如何处理颜色渐变?
最直接的想法,是直接将像素按照位置对应。这样的方法称为直接变形法。它的思想很简单,两张图片大小相同,对于位置一样的像素,根据中间帧位置不同加权进行插值,从而得到变形的中间帧图像。它本质上是让S逐渐消失,让D逐渐出现。在中间过程中S和D同时出现重叠交叉,不够自然,也没有渐变的感觉。下图是一张直接变形法的例子:

我们在这里重点要介绍的是,基于特征的图像变形法。
在这个方法中,像素之间的对应关系不会再是简单的根据pixel的位置对应了,而是通过分析图像的特征建立起对应关系。在该对应关系的基础上,将几何变形和颜色变形结合起来。
有一个最直接的做法,是用户标注一组图像的基网格控制点的对应关系,然后做插值,不过这样人需要做的工作量太大,如下图:

Beier和Neely提出了一种新的解决方法,只需要让用户标注一些对应的向量,然后插值图像S和D像素之间的对应关系,再根据对应关系进行插值,得到中间帧图像。如下图:

下面简单介绍以下Beier & Neely算法的内容。
首先考虑单个控制向量的情况,如下图:

\(P’Q’\)和\(PQ\)分别是S和D上对应的参考向量。对于D上的一点\(X\),要计算\(X\)在S上的对应点\(X’\)。可以看到上图中,对于D中任一点,有\(v\)和\(u\)两个量决定了它相对于控制向量的位置,因此对于S中也同样可以这样来确定\(X’\)的位置。我们保持\(X\)到参考向量\(PQ\)的投影距离以及投影点在\(PQ\)的相对位置不变,可以得到下面的式子: \[ u = \frac{(X - P)\cdot(Q - P)}{ \Vert Q - P \Vert^2}\\ v = \frac{(X-P) \cdot Perpendicular(Q-P)}{\Vert Q - P\Vert}\\ X' = P' + u \cdot (Q'-P') + \frac{v \cdot Perpendicular(Q' - P')}{\Vert Q' - P'\Vert} \] 如果控制向量有多个,为了计算\(X\)的对应点\(X’\),简单针对每个单独的控制向量计算\(X\)的对应点:\(X_1’,X_2’,…,X_k’\),最后将它们加权相加即可: \[ X' = w_1 X_1' +w_2 X_2' + ... + w_k X_k'. \] 这里比较复杂的问题就是如何确定权重。
假设有多个控制向量\(P_iQ_i\),如下图:

他们提出的权重计算方法如下: \[ w_i = \left(\frac{len^p(P_iQ_i) }{a + dist}\right)^b \] 其中\(len(P_iQ_i)\)是\(P_iQ_i\)的长度,dist是\(X\)到\(P_iQ_i\)的距离,而\(a,b,q\)都是正常数。
因此,使用Beier & Neely算法可以进行较为容易而且自然的图像变形,步骤如下:
- 要计算S和D之间的任一中间帧图像M,首先插值出M中所有的控制向量(使用naive的插值方法得到)
- 对于M中的任一点\(X\),使用上述算法,找到\(X\)在S和D中的对应点\(X_s\)和\(X_d\)
- 将\(X\)的颜色按照\(X_s\)和\(X_d\)的颜色混合,权重根据M的位置决定
通过这个算法得到的效果如下:

这个算法出自于paper:
feature-based
image metamorphosis。
形状混合(Shape Blending)
二维图像动画都可以简化为多边形处理,二维形状混合实际上是在两个关键帧的多边形之间插入中间多边形,需要解决的问题主要是顶点对应问题以及插值路径问题,使得两个帧之间的变化更加自然合理。
在有了顶点对应关系的情况下,需要关注的就是对应顶点之间的插值路径问题。这里将介绍3个算法:顶点插值法,几何内在参数法以及边向量混合法。
顶点插值法
给定具有相同顶点个数的两个多边形: \[ P = [P_1,...,P_m],Q = [Q_1,...,Q_m] \] 同时这两个多边形顶点之间有对应关系:\[。则顶点插值法简单使用对应点间的线性插值来实现形状混合: \] \[\begin{aligned} R(t) &= (1 - t)P+tQ\\ &= [(1 - t)P_1 + tQ_1 ,...,(1 - t)P_m+tQ_m] \end{aligned}\]$$ 顶点插值法简单快速,但是容易导致不自然甚至会出现边萎缩的变化过程,如下图:
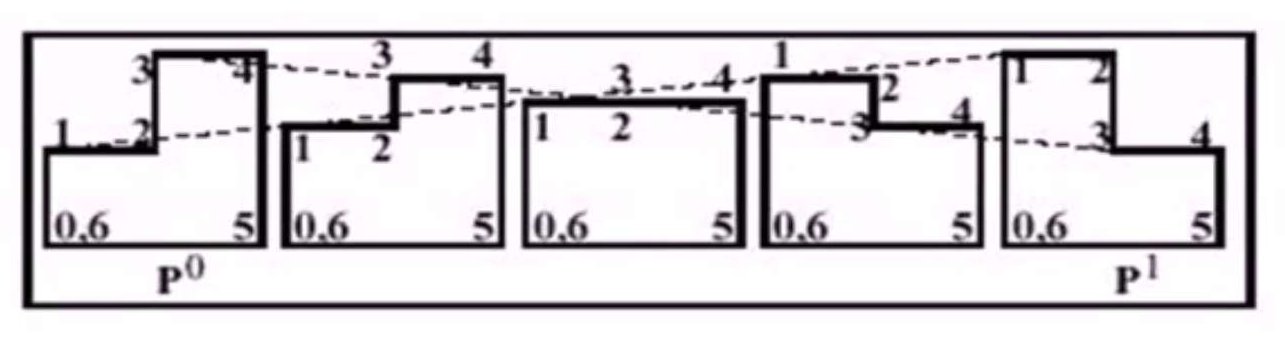
可以使用顶点重新编号和插入新顶点的策略来消除退化情况,但是很难获得最理想的混合效果:
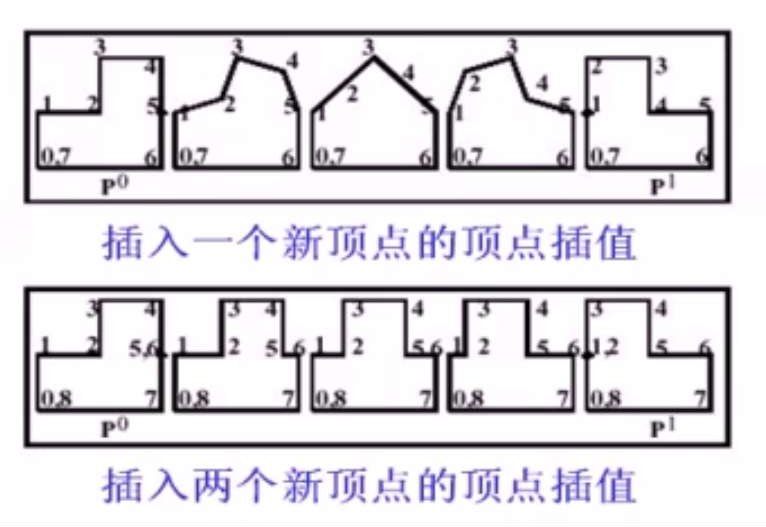
下面是改变顶点编号对应关系的效果:

几何内在参数法
几何内在参数法与顶点插值法不同,它不对顶点直接插值,而是插值出多边形的边和角,然后再计算顶点的位置,这样对于形状的保持会比直接插值顶点要好很多。如下图:

上图中,对于中间帧的插值计算如下: \[
\theta _i(t) = (1-t)\theta _{Ai} + t \theta_{Bi}\\ L_i(t) = (1-t)L_{Ai}
+ tL_{Bi}
\] 几何内在参数法的一个问题是,它这样插值出来的多边形\(L_i\)以及顶点\(\theta_i\)不一定能围成一个封闭多边形,如下图:

有一个解决办法是,保证顶角\(\theta_i\)不变,修改边长\(L_i\)的值: \[ L_i(t) = (1-t)L_{Ai} + tL_{Bi} +S_i \] 这个方法被称为所谓的tweak算法。
为了保持多边形的封闭,对于\(S_i\)有两个线性约束: \[ \varphi_1 (s_0,s_1,...,s_m) = \sum_{i=0}^m [(1-t)L_{Ai} + tL_{Bi} + S_i]\cos \alpha_i = 0\\ \varphi_2 (s_0,s_1,...,s_m) = \sum_{i=0}^m [(1-t)L_{Ai} + tL_{Bi} + S_i]\sin \alpha_i = 0\\ \] 在这两个约束下,我们希望所有长度\(L_i\)的改变\(S_i\)尽可能的小,因此这就构成了优化问题,使用各种优化算法可以解决。下面是tweak算法和顶点插值法的比较:

边向量混合法
几何内在参数法运算量比较大,速度较慢,而边向量混合法通过对边长向量直接进行插值操作,在实时计算的同时可以保证边长的单调性。
现在假如两个多边形的边向量分别为:\(\{a_1,…,a_m\}\)和\(\{b_1,…,b_m\}\),并且有对应关系$$对边向量进行插值过程如下:
- 如果有\(a_i,b_i\)构成的三角形的两个底角中有一个为非锐角,直接进行线性插值: \[c_i(t) = (1-t)a_i +tb_i\]
- 如果该三角形两个底角都是锐角,那么希望它有一个弧形的变换过程,可以使用Bezier曲线插值: \[c_i(t) = (1-t)^2a_i +(1-t)tp_i + t^2b_i\] 这时候需要确定点\(p_i\)(一个控制顶点): \[p_i = (a_i + b_i) \times (1 + \lambda_i)/2\]
当然,边向量混合法也需要保持多边形的封闭性,也就是: \[ c_1(t)+...+c_m(t) = 0 \] 在文章计算机动画的向量混合方法中,作者通过对插值方程进行松弛,指出在一定条件下,可以在满足多边形封闭性的同时依旧保持边长的单调性。下面是边向量混合法的例子:
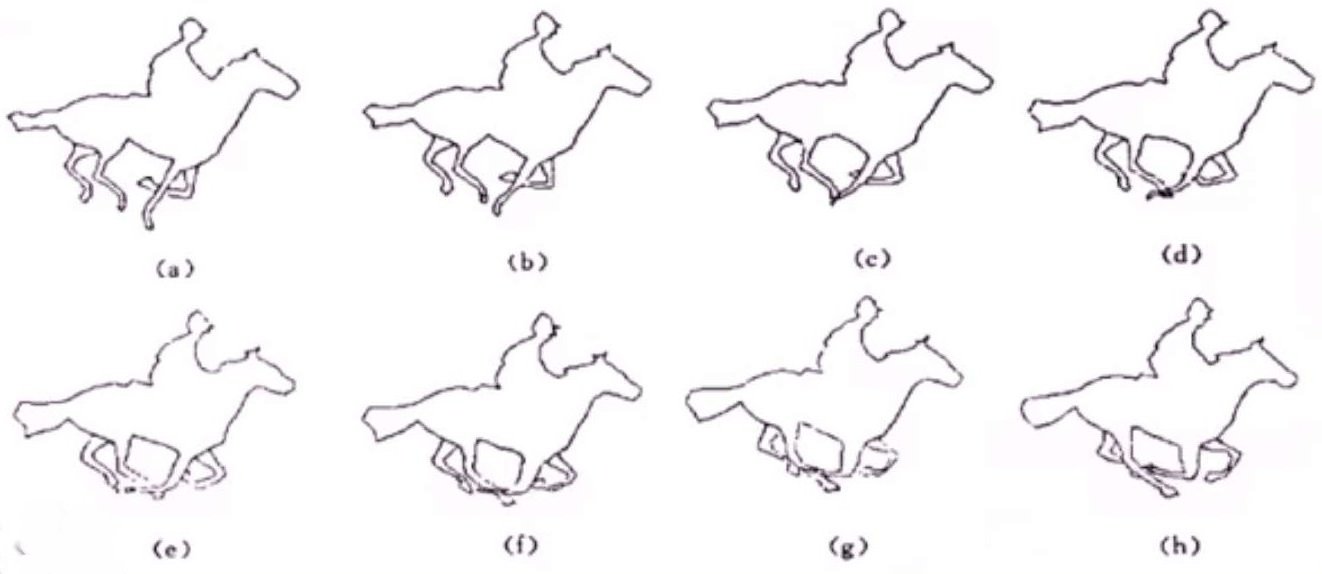
三维动画
关键帧动画
关键帧实际上不光在三维动画中有,实际上上面说的二维的形状混合也是为了填充关键帧之间的局部帧的变化。关键帧动画实际上最早在传统动画中有用到了,因为大师级的画师很贵,在做动画时,大师只用绘制关键帧,而对于关键帧之间的局部帧(自然的过渡过程),可以让一般的画师来完成。
而在三维动画中,希望中间的过渡也是用计算机生成,影响画面的产生可以成为关键帧的参数,如位置,旋转角,纹理等。
中间的过程也会有两种情况,一个是刚体的运动。它需要解决的问题是,给定一个运动轨迹,求物体在某一帧的位置,而运动轨迹可以使用参数样条标识,而直接对参数空间进行等间隔采样可能会引起运动的不均匀性,更好的做法是对样条进行弧长参数化。
变形物体的动画
除了刚体变换,还有一个非常重要的是变形物体的动画,因为生活中绝对刚体是不存在的,物体的受力总会伴随着形变。对于变形动画主要方法有Barr的变形变换,轴变形,面变形等,而最有名的方法叫自由体变形方法(FFD)。
这里我们详细介绍FFD算法。
自由体变形技术
FFD方法提出的很早,但是直到现在也是非常重要的变形方法。它的思想是:将变形物体嵌入一个柔软的实体中,这个实体通常比较简单,比如长方体等,而这个包含嵌入物的实体的变形,使得嵌入物发生相应的形变,如下图所示:
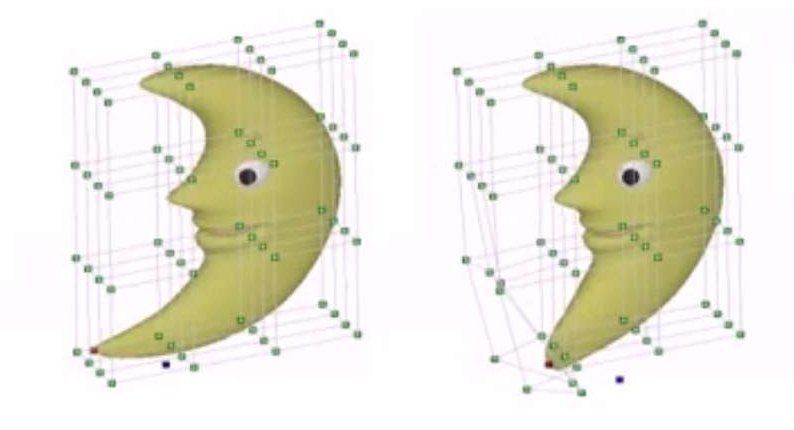
FFD算法分4个步骤:
- 构造一个足够大的三参数自由体,如张量积Bezier体
- 将欲变形的物体嵌入到自由体中,变形物上各点都可以对张量积Bezier体反求参数
- 张量积Bezier体通过改变控制顶点来作变形
- 对变形物体上各点,由参数按新控制顶点计算点变形后的新位置,由此得到新的变形体
对于基于NURBS基函数的FFD方法,基函数为: \[ V(u,v,w) = \frac{\sum_{i=0}^l \sum_{j=0}^m \sum_{k=0}^n V_{i,j,k}W_{i,j,k}B_{i,p}(u)B_{j,q}(v)B_{k,r}(w)}{\sum_{i=0}^l \sum_{j=0}^m \sum_{k=0}^nW_{i,j,k}B_{i,p}(u)B_{j,q}(v)B_{k,r}(w) }, 0\leq u ,v,w \leq 1 \] FFD虽然很容易变形,但是对于一个物体如何作制定形状的变化没那么容易,因为它控制的是控制顶点,而不会直接操作嵌入物的点。因此下面我们介绍一种FFD的改进,被称为DFFD(Direct Manipulation of FFD)。在DFFD中,用户可以直接选定物体上的一些点,给定它的目标变换位置,接着让算法求出控制点需要进行的变换,在对整个嵌入物进行改变。可以看到DFFD对于用户更友好。DFFD的思想如下:
假如希望一个点\(S\)变形后成为\(T\),那么我们实际上相当于需要计算控制顶点的位移\(\delta_{i,j,k}\),使得: \[ \begin{aligned} T &= \sum_{i,j,k = 0}^{l,m,n}(P_{i,j,k} +\delta_{i,j,k} )R_{i,j,k}(u_s,v_s,w_s)\\ &= S+ \sum_{i,j,k = 0}^{l,m,n}\delta_{i,j,k}R_{i,j,k}(u_s,v_s,w_s) \end{aligned} \] 上面的构成了一个约束,而我们希望在这个约束下,尽量减少变化量的值,也就是: \[ \min\sum_{i,j,k = 0}^{l,m,n} \Vert \delta_{i,j,k} \Vert^2 \] 使用拉格朗日乘数法,最后发现它是有显示解的: \[ \delta_{i,j,k} = \frac{R_{i,j,k}(u_s,v_s,w_s)}{\sum_{i,j,k = 0}^{l,m,n}R^2_{i,j,k} (u_s,v_s,w_s)}(T-S) \] 这是一个很好的消息,因为在计算机中一般来说显示解比慢慢去优化快很多。不过这是只改变一个点的情况,如下图:

使用DFFD进行连续变形的时与路径无关,也就是变回来之后,控制顶点还是原来的位置。
如果我们想要改变多个点,现在希望改变\(h\)个点,这时候就会有\(h\)个方程组。这时候的求解过程就没有显示解了。对于每个点,都有: \[ \begin{aligned} T_f &= \sum_{i,j,k = 0}^{l,m,n}(P_{i,j,k} +\delta_{i,j,k} )R_{i,j,k}(u_f,v_f,w_f)\\ &= S_f+ \sum_{i,j,k = 0}^{l,m,n}\delta_{i,j,k}R_{i,j,k}(u_f,v_f,w_f) \end{aligned} \] 这时候构造拉格朗日乘数,就会需要\(h\)个\(\lambda\): \[ L = \sum_{i,j,k = 0}^{l,m,n} \Vert \delta_{i,j,k} \Vert^2 + \sum_{f=1}^h\left( T_f - S_f - \sum_{i,j,k = 0}^{l,m,n}\delta_{i,j,k}R_{i,j,k}(u_f,v_f,w_f) \right) \] 当然,我们不希望求解这样方程,希望有那样一种方法,可以将多个点的改变转化成一连串单个点的转换,这个做法被称为多点约束条件的分解。有这样一个定理,一个包含了\(h\)个点约束条件下的DFFD问题,可以依次分解为\(h\)个单点约束条件下的DFFD问题串接而成,这个定理可以帮助我们做出多点约束条件下DFFD问题的显式解。下面是多点改变的DFFD示例:

在NURBS函数的DFFD方法中,我们除了改变控制点的位置,也可以改变权值(还记得NURBS是通过权值来实现比B样条更优的性质),和改变点的位置一样,对于权值我们有: \[ T=\frac{\sum_{i, j, k=0}^{t, m, n} P_{i, j, k}\left(W_{i, j, k}+\varepsilon_{i, j, k}\right) B_{i, p}(u) B_{j, q}(v) B_{k, r}(w)}{\sum_{i, j, k=0}^{l, m, n}\left(W_{i, j, k}+\varepsilon_{i, j, k}\right) B_{i, p}(u) B_{j, q}(v) B_{k, r}(w)} \] 类似,我们优化: \[ \sum_{i, j, k=0}^{l, m, n}\left\|\varepsilon_{i, j, k}\right\|^{2} \] 通过拉格朗日乘数,得到方程组: \[ \left\{\begin{array}{l}{(T-S) \sum_{i, j, k=0}^{l, m, n} W_{i, j, k} B_{i, j, k}\left(t_{s}\right)+\sum_{i, j, k=0}^{l, m, n}\left(T-P_{i, j, k}\right) \varepsilon_{i, j, k} B_{i, j, k}\left(t_{s}\right)=0} \\ {\varepsilon_{i, j, k}=-\frac{\lambda}{2}\left(T-P_{i, j, k}\right) B_{i, j, k}\left(t_{s}\right), 0 \leq i \leq l, 0 \leq j \leq m, 0 \leq k \leq n}\end{array}\right. \] 下面是基于权值修改的例子:
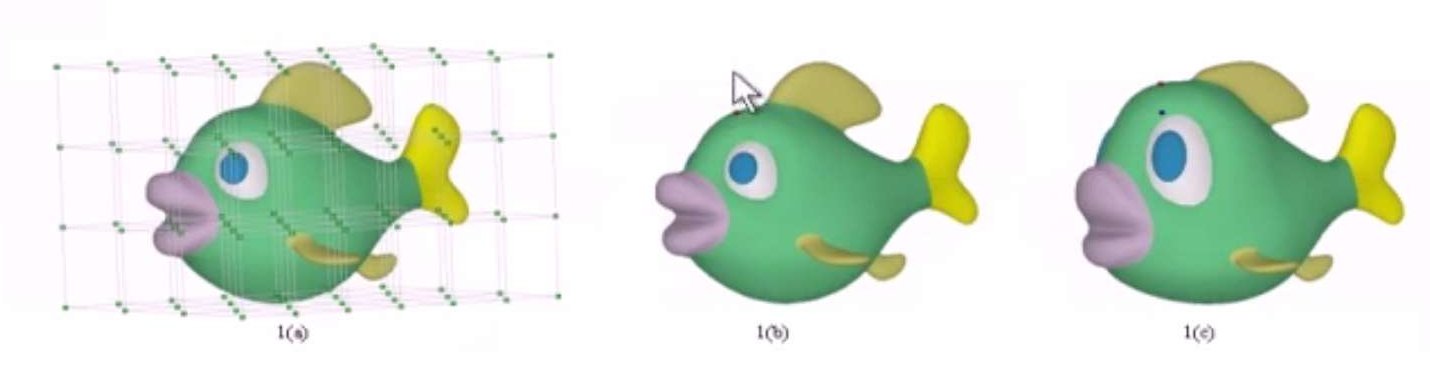
FFD算法的文章出自于:Free-Form Deformation
DFFD算法:Direct Manipulation of Free-Form Deformations
过程动画
过程动画指的是用一个过程去控制物体的动画。过程动画也涉及到物体的变形,但是与柔性体的变形不一样,过程动画基于一定的数学模型或者物理规律,比如粒子系统就是过程动画的典型代表。
关节动画和人体动画
人体与动物的三维动画至今依然是研究的热点,没有得到很好的解决。人体有200以上的自由度以及非常复杂的运动,肌肉也随着人体的运动而变形。关节动画与人体动画通常涉及运动学与动力学的知识。关于人体动画的有个有趣的研究叫voice puppetry,它根据音调来选择人的五官动作,从而实现绘声绘色的“演讲”效果。
其他的,由于人工智能的兴起,还有一些根据人工智能产生物体行为的动画,比较有名的比如晓媛的鱼,对于鱼赋予了智能,因此下一帧的样子我们并不清楚,而是鱼“自己”决定的。