数字图像处理——图像增强

Posted on 2019-04-22 Edited on 2023-10-22 In 数字图像处理

从这周开始进行数字图像处理这门课程。实际上图像处理，也是计算机图形学的一个分支。我们生活中使用的各种美图ps等等都是属于图像处理的范畴。这次介绍图像处理中图像增强的部分。

图像获取是将模拟连续信号转化成数字信号的过程，而在采样过程中，有一个著名的定律：奈奎斯特采样定律。它要求采样的频率是原始信号频率的2倍以上，才能保证不丢失信息。获取到图像后，就有很多后续的操作了。

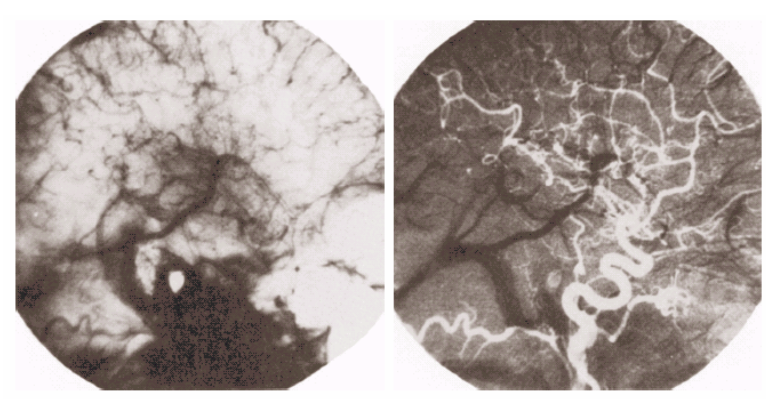
实际上，图像增强是一个很大的范畴。简单来说，是因为我们的目的不同，所以增强的方法也不同。简单的来说，图像增强在空间域上分为3类：点操作，全局操作，以及块操作（更熟悉的名字，叫滤波），除了空间域，在频域上也有很多相关的算法。图像增强经常应用到各种特征提取的预处理阶段，也常常应用到生活中，下图是图像增强的几个例子：

在这里介绍几个很重要的图像增强相关算法。对于空间域上的操作，我们可以用下面的式子来表示： \[ g(x,y)= T[f(x,y)] \] 上式中，$f(x,y)$表示图像，$(x,y)$表示图像的像素位置，因此一个图像经常可以用矩阵来表示。而$f$表示的是像素的值，这个值可以是多种的，比如灰度值，RGB值，亮度值，甚至是深度值（那么这个图是深度图）。$g(x,y)$表示增强后的图像，而$T$表示这个操作。操作$(x,y)$位置的像素时候牵涉得到的其他像素值的范围，决定了这个值是点操作还是块操作还是全局操作，如下图是一个滤波的一般范围（$3 \times 3$，也可以是别的大小）：

点操作（point operation）

点操作，也就是对每个像素的处理，只由自己决定，这意味着它不会受到位置影响，只受到值的影响，因此可以简单的写成：$s = T(r)$。

裁剪和阈值化（clipping and thresholding）

最简单的点操作算法（可能也是最简单的图像处理算法）是二值化，它是阈值化的一种。二值化指的是设定一个阈值$t$，当值大于$t$设定为$255$，当值小于$t$的时候设定为$0$。因此最后整个图像只包含两个值。而裁剪就更灵活一点,可以选取某段范围内的值不改变，不过也会根据阈值，比如大于$t$的设定为某个值，小于则为原来的值。

图像反转（image negatives）

做图像反转，是因为对于人眼来说，黑暗中亮的物体和亮中暗的物体效果是不一样的。下面是一个图像反转的例子：

计算过程为： \[ s = L-1 -r,r \in [0,L-1] \] ### Log转换

还有一系列根据$r$计算$s$的算法，使用log函数： \[ s = c\log(1+r) \] 下面这张图展示了经过log转换以及图像反转后的值：

指数转换

另外一个比较重要的是根据指数计算新的值： \[ s = c(r+\epsilon)^v \]

实际上这些转换都非常简单，我们甚至可以自己构造更多的函数来达到想要的效果。上图中，如果$L$表示亮度或者灰度值，那么$v>1$的情况下，会使得整个图变暗，相反会使得整个图变亮，需要注意的是，上面的$r$值是经过处理的，因为我们要保证$log$(1+r),(r)^v$的值域为$[0,1]$，因此这里的$r$并不是原始的值，而是经过了归一化处理。下面的图像就是整个色调变亮：

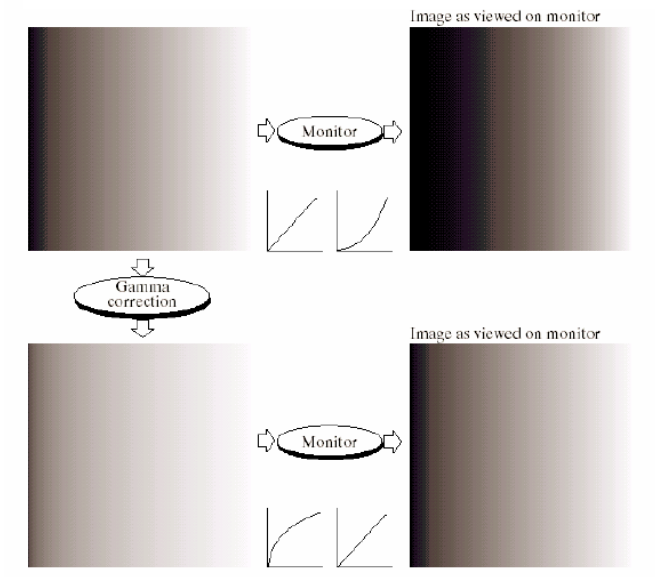
一个指数转换的例子是伽马校正（gamma correction），一般来说ps操作可能会遇到：

另外比如对比度增强也会用到指数转换：

上面的图对应$c=1,v=0.4,0.6,0.3$的效果，图像整个变亮，而且经过指数转换，颜色深的部分的对比度会增加，因此从人眼角度可以显示更多的细节。

上图对应$c=1,v=3.0,4.0,5.0$，同样的道理，整个图像变暗，但是对于颜色较亮的部分对比度会增加。

分段线性转换（piecewise linear transformation）

我们可以根据分段线性转换来达到想要的效果。比如之前的提升的都是暗色的部分或者亮色的部分，如果想要提升中间部分的对比度，容易想到的是使用sigmod函数，或者使用分段线性函数： \[ s =\left\{ \begin{matrix} \alpha r, 0 \leq r < a\\ \beta(r - a)+v_a,a \leq r < b\\ \gamma(r - b)+v_b, b \leq r < L \end{matrix} \right. \] 我们对$[a,b]$范围内的值延伸至$[v_a,v_b]$，这其中： \[ \alpha = \frac{v_a}{a},\beta = \frac{v_b- v_a}{b-a}, \gamma = \frac{L - v_b}{L-b} \] 效果如下图（右下角是二值化）：

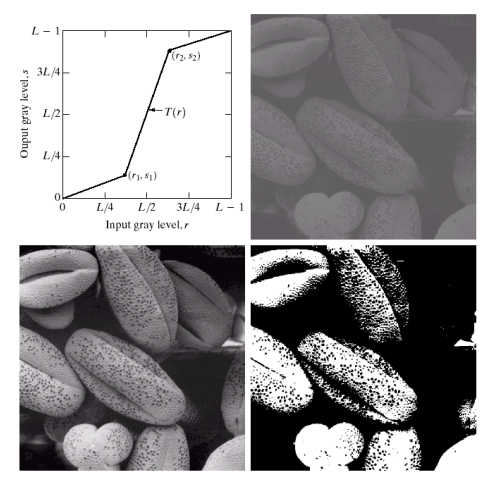
灰度级切片操作（gray level slicing）

使得处于某部分范围内的值着重显示。

bit平面的切片操作(bit plane slicing)

我们知道一般$r$是有8个bit表示的： \[ r = k_1k_2...k_8 \] 做下面的处理： \[ s =\left\{ \begin{matrix} L, \text{if n-th significant bit = 1}\\ 0,\text{otherwise} \end{matrix} \right. \] 下面是一个选取不同的significant bit的例子：

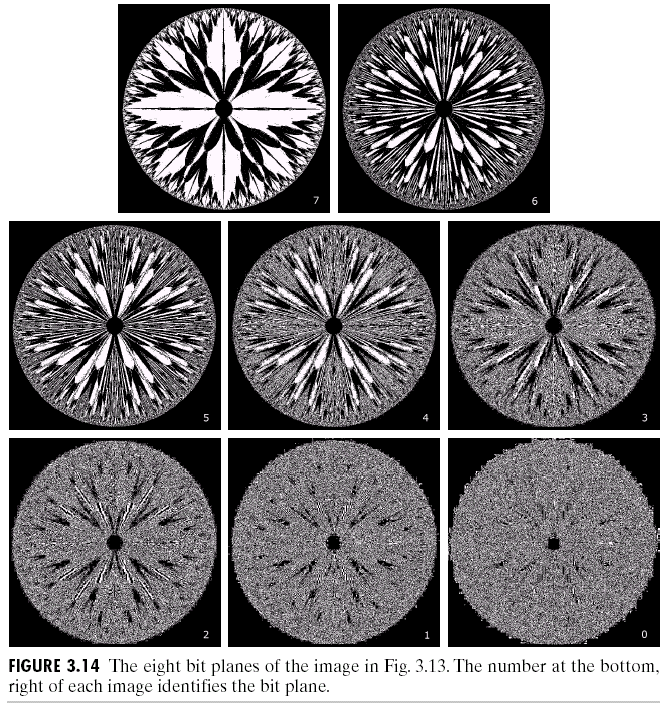
可以看到的是，可以表达的细节更少，但是不同的significant bit的选择，会带来神奇的效果。

全局操作

全局操作指的是新的像素值，是由整张图片决定的。这里介绍一个频率直方图上的操作（histogram），在空间域上它被归属于全局操作，实际上它也是频域上的操作。

一个图像的频率直方图如下：

直方图高度代表有多少个像素是这个值。有了直方图就有较多的操作了，比如直方图分布不均匀，如何将直方图变得均匀一点？也就是我们希望对像素值进行映射，需要一个映射函数。映射函数必须满足两点：

必须不能影响原来值的大小关系，也就是是严格单调递增函数
值域不能越界

直方图均衡化（histogram equalization）

为了解决这个问题，首先我们要知道直方图实际上是概率分布图，考虑连续的情况。对于一个连续的概率密度函数，如何做映射到均匀分布？这里有一个非常巧妙的方法。我们选择了概率中的累积分布函数。它满足了上面最基本的要求。下面分析为什么它能使得分布均衡化。

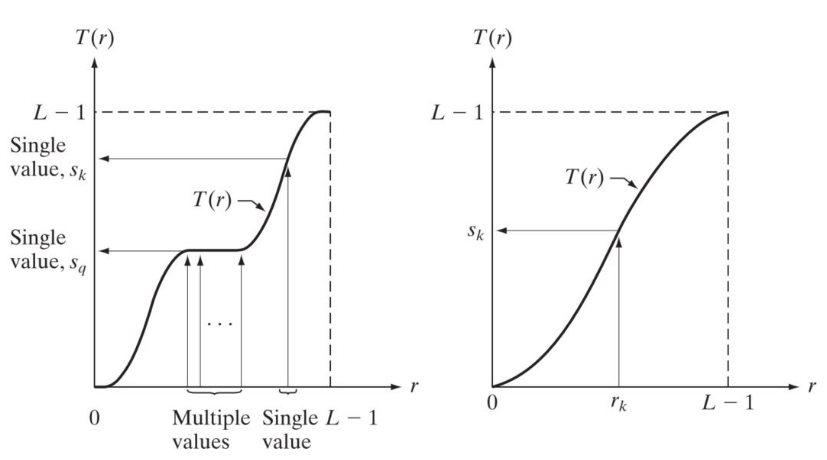
上图中，如果非严格单增，可能原来多个不相等的值映射到相同的值。

我们希望做到下面的映射：

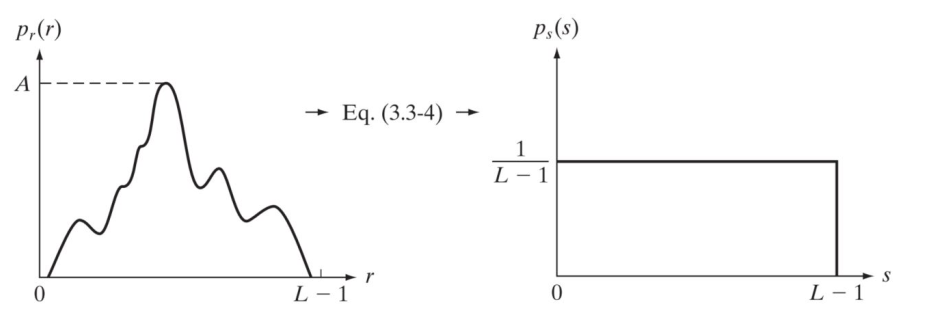
令： \[ s= (L-1)\int_0^r p_r(w)d_w \] 则： \[ \frac{ds}{dr} =(L-1) p_r(r) \] 这时候求$p_s(s)$，我们知道： \[ p_s(s) = p_r(r)\lvert\frac{dr}{ds}\rvert \] 这一步比较难懂一点。实际上这里是概率论相关的内容。假设有两个随机变量$X,Y$，它们的概率密度函数分别为：$f_X(x),f_Y(y)$，累积分布函数分别为：$F_X(x),F_Y(y)$。而且$X,Y$满足下面的关系： \[ Y = g(X) \] 且$g$是单调可导函数。那么该函数具有反函数： \[ X = g^{-1}(Y) \] 根据定义： \[ \begin{aligned} F_Y(y) &= P(Y\leq y)\\ &= P(g(X) \leq y)\\ &= P(X \leq g^{-1}(y))\\ &= \int_{0}^{g^{-1}(y)}f_X(w)dw\\ &= F_X(x)\vert_0^{g^{-1}(y)}\\ &= F_X(g^{-1}(y)) - F_X(0) \end{aligned} \] 上式两侧同时对$y$进行求导： \[ f_Y(y) = f_X(g^{-1}(y)) \frac{dg^{-1}(y)}{dy} = f_X(x)\frac{dx}{dy} \] 反函数的导数是原来导数的倒数。当函数是单调减函数时，$\frac{dx}{dy}<0$，而概率密度函数应该始终非负，因此需要加上绝对值。
则： \[ p_s(s) = p_r(r)\lvert \frac{dr}{ds} \rvert = \frac{1}{L-1} \] 而这正是均匀分布的特征。

对于离散的情况，也就是我们需要处理的情况： \[ \begin{aligned} s_k &= T(r_k) = (L-1)\sum_{j=0}^kp_r(r_j) \\ &= (L-1)\sum_{j=0}^k\frac{n_j}{n}\\ &= \frac{L-1}{n}\sum_{j=0}^k n_j \end{aligned} k = 0,...,L-1 \] 离散情况下，我们无法保证概率密度函数一定是严格单调增的，但是这个实际上不会太影响，没有严格单调增是因为某些像素值在图片中是不存在的，对该值的映射也就无所谓了。需要注意的是，有可能会将多个值映射到一个值上，因为像素值是整数，我们必须要做取整的操作。

在离散情况下，得到的不会是绝对的均匀分布。由于离散情况下，每个值对应一个值（或者多个），因此均衡化后各个对应值的频率不会减少，但是会将过于集中的分布拉开。
下面是一个直方图均衡化的例子：

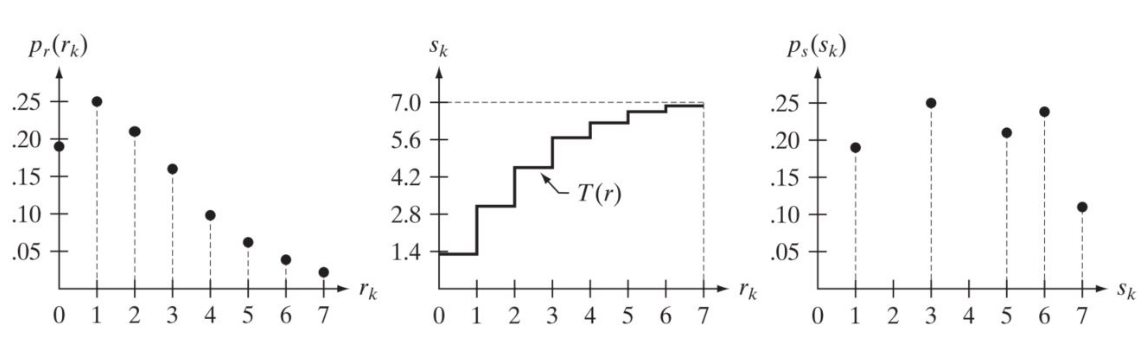
直方图规定化（histogram specification）

直方图均衡化并不一定总是符合我们的要求。有时候我们不希望分布的太均匀，而是希望直方图分布照着我们想要的样子来。这时候我们需要提供两张图片，一张原始图像，一张目标图像，表示希望原始图像映射后与目标图的直方图类似。原始图像与目标图像的概率分布分别为：$p_r(r)$与$p_z(z)$。对于规定化，首先做的是均衡化。分布对两张图像都进行均值化： \[ s = T(r) = (L-1)\int_0^r p_r(w)d_w\\ v = G(z) = (L-1)\int_0^z p_z(w)d_w \] 分别表示均衡化后的原始图像和目标图像。实际上我们可以根据均值化后的结果，求出原始图像： \[ r = T^{-1}(s) \] 由于目标图像和原始图像都进行了均值化处理，因此他们应该具有相同的概率密度（离散情况下不一定会完全相同）： \[ p_s(s) = p_v(v) \] 因此可以使用目标图像均值化后的结果来得到原始图像规定化的样子： \[ z = G^{-1}(v) = G^{-1}(s) \] 在离散情况下，这个问题更好解决，只要根据映射反向回去即可。但是需要注意的是，映射并不是一一对应的，原来的多个值映射到一个值，因此反向的时候，可能有多个值找不到对应的映射，这时候只要简单的找附近的值对应的映射就可以了。

上面就是直方图规定化的内容，可以看到均值化是规定化的基础。

除了上面介绍的之外，还有图像之间的and，or以及sub等等操作，都是非常简单的内容。下面是几个例子：

下面会用python的代码实现一下直方图均衡化和直方图规定化：

# python histogram equalization and specification
import math
import numpy as np
from PIL import Image
from pylab import *

def equalization(im):
    obj = im.flatten()
    sta = [0 for i in range(256)]
    for i in obj:
        sta[i] = sta[i]+1
    sta = [i /len(obj) for i in sta ]

    updated = []
    integral=0.0
    for i in sta:
        integral += i
        updated.append(int(integral * 255))
    nim = np.array(im)
    for i in range(len(im)):
        for j in range(len(im[i])):
            nim[i][j] = updated[im[i][j]]
    return nim,updated

def specification(im,im_s):
    nim,updated1 = equalization(im)

    nim_s,updated2 = equalization(im_s)
    updated = [-1 for i in range(256)]
    for i in range(256):
        if updated[updated2[i]]==-1:
            updated[updated2[i]] = i
    for i in range(256):
        j=1
        while updated[i] == -1:
            updated[i] = updated[(i+j)%256]
            if updated[i] == -1:
                updated[i] = updated[((i-j)+256)%256]
            j+=1
    final = np.array(im)
    for i in range(len(im)):
        for j in range(len(im[i])):
            if updated[im[i][j]]!= -1:
                final[i][j] = updated[im[i][j]]
    return final

im = np.array(Image.open("./image_black.jpg").convert("L"))
nim = equalization(im)[0]
im_s = np.array(Image.open("./object1.jpg").convert("L"))
final = specification(im,im_s)

'''Image.fromarray(im).show()
Image.fromarray(nim).show()
Image.fromarray(im_s).show()
Image.fromarray(final).show()'''
figure()
#hist(im.flatten(),256)
#hist(nim.flatten(),256)
hist(im_s.flatten(),256)
hist(final.flatten(),256)
show()

原始图像为：

它的灰度图为：

经过直方图均衡化之后的效果:

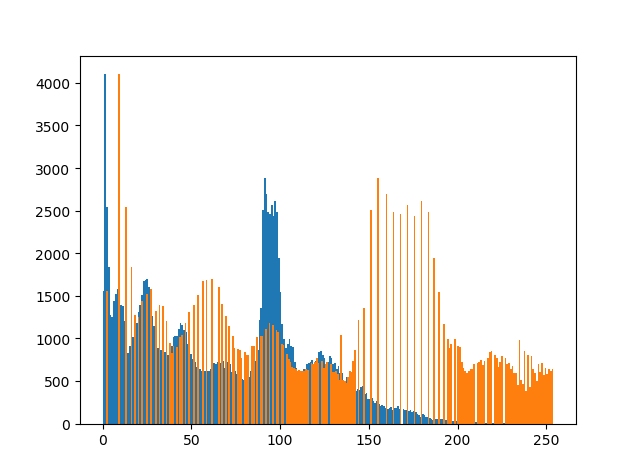
均衡化前后的直方图对比（原来的直方图为蓝色，均衡化后的为黄色）：

对于规定化，需要选择目标图像。为了更好地显示效果，我选了两个目标图像来分别作规定化。第一个目标图原图为：

第一个目标图灰度图如下：

经过规定化之后，效果如下：

可以看到的是，由于我选了宇宙图，黑色占了大多数，因此整个图的色调会变暗很多。而目标图的直方图（蓝）和规定化后的直方图（黄）对比如下：

对于第二个规定化，我选择了蓝天白云的风景图，可以看到，这个应该会让整个图的色调变亮。第二个目标图原图为：

第二个目标图灰度图为：

经过规定化后，效果为：

目标图的直方图（蓝）和规定化后的直方图（黄）对比如下：

图像的放大缩小（resize）

图像的放大和缩小也是一个图像的基本操作。图像的缩小和放大会有比较多的插值方法。最简单的就是不做差值，直接复制原来的像素或者采样。这样效果很差。而比较有名的插值方法有最邻近插值（nearest），双线性插值（bilinear），双立方插值（bicubic）等等，一般来说这些方法都会被直接实现在各个程序包中了。比如在matlab的imresize函数以及PIL中Image的resize函数，我们可以选择不同的插值方法来达到不同的效果。这些算法背后就是数学的插值方法，这里就不多介绍了。