SLAM——LIO-SAM
Lio-sam: https://github.com/TixiaoShan/LIO-SAM
Lio-sam has a similar code structure with A-LOAM (more similar to LeGO-LOAM, but without ground points). However, they are very different. A-LOAM doesn't have a pose graph optimization in back-end. It uses current scan to matching the global map, which can lead to drift over a long distance scanning. LIO-SAM uses a lidar-IMU odometry, and it adopts a factor graph for multi-sensor fusion and global optimization. If you want to fuse other sensors it would be much easier. Also, it supports loop closure detection.
From the demo (https://www.youtube.com/watch?v=A0H8CoORZJU), we could see that LIO-SAM is really robust to arbitrary rotation and has high localization accuracy. At any time, the robot state can be formulated as:
\(\mathbf R\) is the rotation matrix, \(\mathbf p\) is the position, \(\mathbf v\) is the speed and \(\mathbf b\) is the IMU bias.
\[ \mathbf{x}=\left[\mathbf{R}^{\mathbf{T}}, \mathbf{p}^{\mathbf{T}}, \mathbf{v}^{\mathbf{T}}, \mathbf{b}^{\mathbf{T}}\right]^{\mathbf{T}} \]
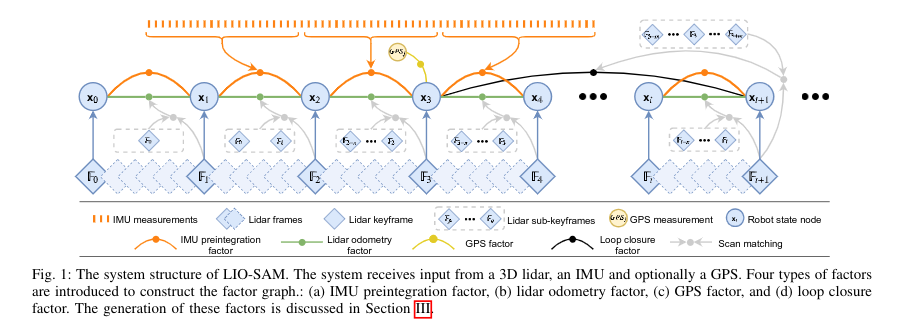
There are 4 types of factors in LIO-SAM: (a) IMU preintegration factors, (b) lidar odometry factors,(c) GPS factors, and (d) loop closure factors.
We denote the world frame as \(\mathbf W\) and the robot body frame as \(\mathbf B\). \(\mathbf T_t^{\mathbf {BW}}\) is the transformation from world
IMU Preintegration
IMU will provide angular velocity and acceleration:
\[ \begin{array}{l}\hat{\omega}_{t}=\omega_{t}+\mathbf{b}_{t}^{\omega}+\mathbf{n}_{t}^{\omega} \\\hat{\mathbf{a}}_{t}=\mathbf{R}_{t}^{\mathbf{B W}}\left(\mathbf{a}_{t}-\mathbf{g}\right)+\mathbf{b}_{t}^{\mathbf{a}}+\mathbf{n}_{t}^{\mathbf{a}}\end{array} \]
where \(\hat{\omega}_t\) (angular velocity) and \(\hat{\mathbf{a}}_{t}\) (acceleration) are the raw IMU measurements in \(\mathbf B\) at time \(t.\) \(\mathbf b_t\) and \(\mathbf n_t\)are bias and white noise respectively. \(\mathbf R_t^{\mathbf{BW}}\) is the rotation matrix from \(\mathbf W\) to \(\mathbf B\). \(\mathbf g\) is the constant gravity vector in \(\mathbf W\). And based on those measurements we could infer the motion of robot. The velocity, position and rotation of the robot at time \(t + \Delta t\) can be computed as follows:
\[ \begin{array}{l}\mathbf{v}_{t+\Delta t}=\mathbf{v}_{t}+\mathbf{g} \Delta t+\mathbf{R}_{t}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{t}^{\mathbf{a}}-\mathbf{n}_{t}^{\mathbf{a}}\right) \Delta t \\\mathbf{p}_{t+\Delta t}=\mathbf{p}_{t}+\mathbf{v}_{t} \Delta t+\frac{1}{2} \mathbf{g} \Delta t^{2}+\frac{1}{2} \mathbf{R}_{t}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{t}^{\mathbf{a}}-\mathbf{n}_{t}^{\mathbf{a}}\right) \Delta t^{2} \\\mathbf{R}_{t+\Delta t}=\mathbf{R}_{t} \exp \left(\left(\hat{\omega}_{t}-\mathbf{b}_{t}^{\omega}-\mathbf{n}_{t}^{\omega}\right) \Delta t\right)\end{array} \]
where \(\mathbf{R}_{t}=\mathbf{R}_{t}^{\mathbf{W B}}=\mathbf{R}_{t}^{\mathbf{B W}^{\top}}\). The IMU preintegrated measurements between time \(i\) and \(j\) can be computed as following (Apparently, \(\Delta \mathbf{v}_{i j}\) is not \(v_j - v_i\) ):
\[ \begin{aligned}\Delta \mathbf{v}_{i j} &=\mathbf{R}_{i}^{\top}\left(\mathbf{v}_{j}-\mathbf{v}_{i}-\mathbf{g} \Delta t_{i j}\right) \\\Delta \mathbf{p}_{i j} &=\mathbf{R}_{i}^{\top}\left(\mathbf{p}_{j}-\mathbf{p}_{i}-\mathbf{v}_{i} \Delta t_{i j}-\frac{1}{2} \mathbf{g} \Delta t_{i j}^{2}\right) \\\Delta \mathbf{R}_{i j} &=\mathbf{R}_{i}^{\top} \mathbf{R}_{j} .\end{aligned} \]
See https://arxiv.org/pdf/1512.02363.pdf for detailed derivation.
Lidar Odometry
The lidar odometry in LIO-SAM is similar to Lego-LOAM or A-LOAM. The difference is LIO-SAM adopt keyframe strategy. When a new keyframe \(\mathbb F_{i}\) is registered, it will associate with a new robot state node \(x_{i}\) in the factor graph. The lidar frames between two keyframes will be discarded (Note that the position and rotation change thresholds for adding a new keyframe in LIO-LOAM are \(1m\) and \(10\degree\) respectively). The generation of a lidar odometry factor is described in the following step:
- Sub-keyframes for voxel map. Organize \(n\) most recent keframes as a sub-keyframes and combines their scans as a voxel map \(\mathbf M_i = \left\{\mathbb{F}_{i-n}, \ldots, \mathbb{F}_{i}\right\}\), which includes edge feature voxel map \(\mathbf M^{e}_i\) and plane feature voxel map \(\mathbf M^{p}_i\). Note that \(\mathbf M_i\) will be down-sampled to remove duplicated features.
- Scan-matching. A new keyframe \(\mathbb F_{i+1}\) will be matched to \(\mathbf M_{i}\). The initial transformation \(\tilde{\mathbf{T}}_{i+1}\) is estimated through IMU. The matching process is similar to A-LOAM's lidar mapping module.
GPS
System will still suffer from drift during long-distance navigation tasks. GPS is useful for correcting this long-distance-error. In LIO-SAM, a GPS factor is only added when the estimated position covariance is larger that the received GPS position covariance.
Loop Closure
LIO-SAM use a naive but effective method for loop closure detection based on the Euclidean distance. When a new node \(x_{i+1}\) is registered, we search for the near nodes from the factor graph. For example, \(x_3\) is selected, and we match \(\mathbb F_{i+1}\) with the subkeframe voxel map \(\left\{\mathbb{F}_{3-m}, \ldots, \mathbb{F}_{3}, \ldots, \mathbb{F}_{3+m}\right\}\). If the matching succeed, a relative transformation \(\Delta \mathbf T_{3, i+1}\) will be added into fact graph as a loop closure factor. In LIO-SAM,\(m = 12\) and the search radius is \(15m\).