压缩感知与稀疏模型——Sparse Signal Model

Posted on 2019-07-07 Edited on 2023-10-22 In 压缩感知与稀疏模型

这篇博客介绍第二节课的一些内容。虽然第二章题目是Sparse Signal Model，但是这篇博客还介绍了很多高维下的内容，因此内容是比较杂的。不过这个也就是上课内容的记录，而不是完全按照博客题目分的。

从马毅老师的课上目前学到的最重要的收获，就是遇到一个要优化的问题时从几何的角度来思考，这样能够辅助理解很多东西。

L1-norm为什么能得到更稀疏的点相对于L2来说？

之前的利用sparse representation来进行超分辨的文章中，有一个点是，我们希望得到最稀疏的解，但是L0范数的问题是NP-hard的，因此无法解决，所以将L0问题放宽到了L1问题。我们都知道L1范数能得到比L2范数更稀疏的解，为什么呢？

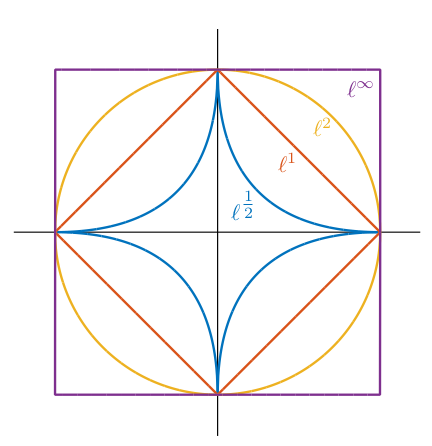
假如有下面待解决的问题： \[ \min \Vert x\Vert_0 \\\text{s.t. }y = Ax \] 对于0范数优化目标是最稀疏的解，是很容易理解的。因为0范数就是不为零的个数。通常解决方法是将上面的问题拓展到1范数： \[ \min \Vert x\Vert_1 \\\text{s.t. }y = Ax \] 现在我们想想，1范数的定义是什么：$Vert x Vert_1 = \Vert x_1 +…+x_n \Vert$。现在考虑三维的情况（更高的维度是类似的，但是我们画不出来），三维坐标下，L1范数的等高线是正8面体，而L2范数的等高线是球体的形状。而$y=Ax$，映射到三维坐标下则是一个平面。

我们在找满足$y=Ax$的情况下最小的$\Vert x \Vert_1$值，实际上就是这个等高线不断扩充，最早正八面体与平面接触的那个点。

而从概率的角度上，正八面体的6个顶点与平面接触的概率是最高的，而这几个顶点相对于其他的点来说是更为稀疏的（只有一个entry非零，如果是边的话则是有两个entry非零）。而球体（L2-norm）边界与平面接触概率是一样的，因此L1范数应该能比L2得到更稀疏的解。

$l^0,l^1,…l^\infty$的可视化

高纬度下的奇怪现象

我们一直想当然的任务高纬度下的数据与低纬度下的是一样的规律，但是实际上维度变高的情况下会出现一些反直觉的现象。

想想二维的圆和三维的球，对于更高的维度，也有一个类似这样的球。我们称围绕直径一圈的圆为赤道，赤道周围计算得到的体积，就占据了整个球的大多数（99%）。这个现象非常的反直觉，而且任意一个这样的赤道，都能得到相同的结论。
在维度变高情况下，$l^1$小于某个值相对于$l^\infty$占得体积越来越小，当维度比较高的时候接近于0。这个是比较好理解的。

还有一些想不起来了。总之在高维情况下，反直觉的现象会出现很多，因此很多的定理都是实践发现后才开始证明。这体现了编程验证能力的重要性。

L0 norm的sparse solution

下面考虑这样一个问题。加入我们有观测量$y \in \mathbb{R}^m$，并且知道矩阵$A$，有$y = Ax_0$，我们的目标是恢复$x_0$。如果我们知道$x_0$是稀疏的，那么选择最稀疏的解$y = Ax$是合理的，也就是我们需要解决的问题为： \[ \text{minimize } \Vert x\Vert_0\\ \text{subject to }Ax = y \] 这里定义一个符号： \[ \text{supp}(x) = \{i| x_i \ne 0\} \subset \{1,,,n\} \] 一个向量的support是一个集合，包含了entry不为0的索引。那么上面的问题就是让我们找到一个有最小support的向量。最容易想到的方法就是尝试所有的可能性。support集合一定是集合$\{1,…,n\}$的子集，因此我们遍历集合$\{1,…,n\}$的所有子集，现在有support集合$I \subseteq \{1,…,n\}$，那么我们可以得到下面一组等式： \[ A_Ix_I = y \] 这里$A_I \in \mathbb R^{m \times \vert I\vert}$是矩阵$A$的子矩阵，由entry索引为集合$I$中的向量组成。这样我们尝试解出$x_I \in \mathbb R^{\vert I\vert}$。如果解存在，将其他的entry设为0即可。算法描述如下图：

利用这个算法做了随机实验，首先随机生成$x_0,A$，其中$x_0$是稀疏的。然后根据$y=Ax_0$得到观察量$y$，接着利用上面遍历的算法对$x_0$进行恢复。得到下面的图：

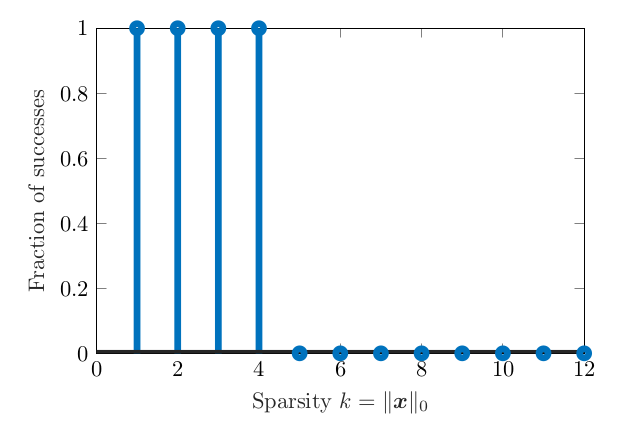
可以发现只要原先向量中非零个数$k$不要太大，也就是足够稀疏，基本上总是能成功找到解。上述实验的size是$5 \times 12$。出现这种现象的原因是什么，有没有数学上的解释？

为了解释为什么L0范数最小化能成功得到解，首先思考一下什么情况下是无法得到解的。假如$x_0 \in null(A)$，也就是属于$A$矩阵的零空间，那么： \[ Ax_0 = 0 = A0 \] 对于上面的情况，最小化L0范数得到的解永远是0向量，无法恢复得到$x_0$。因此我们可以推测，如果$null(A)$包含了稀疏向量，那么我们可能无法恢复原来的稀疏向量。实际上，反过来也是正确的，如果$null(A)$不包含稀疏向量，通过解决L0最小化总是能恢复足够稀疏的原向量。上面的陈述有点让人看不懂，用数学语言说明并证明一下：

现在有原向量$\Vert x_0\Vert \leq k$，并且有： \[ (*) \text{The only } \sigma \in null(A)\text{ with }\Vert \sigma\Vert_0 \leq 2k \text{ is }\sigma = 0. \] 那么如果$x_0$就一定可以被恢复。

首先，假如我们估计量为$\hat x$，那么由于$\hat x$是根据最小化L0范数得到的，因此： \[ \Vert\hat x\Vert_0 \leq \Vert x_0\Vert_0 \leq k \] 定义估计误差为： \[ \epsilon = \hat x - x_0 \] 可以得到： \[ \begin{aligned} \Vert \epsilon\Vert_0 &= \Vert \hat x - x_0\Vert_0 \\ &\leq \Vert \hat x \Vert_0 + \Vert x_0\Vert_0\\ &\leq 2k \end{aligned} \] 而: \[ A\epsilon = A(\hat x - x_0) = y - y = 0 \] 那么根据$(*)$，我们可以得到：$\epsilon = \sigma = 0$。也就是最小化L0范数成功恢复了原来的稀疏向量。

而$(*)$是矩阵$A$的一个性质，因此一个好的矩阵$A$应该是零空间没有稀疏向量的。实际上，要保持这个性质的充要条件是，任意矩阵A的$2k$列是线性独立的。

对于上述现象在线性代数中有一个定理，引入矩阵新的概念Kruskal rank（$krank(A)$），指的是最大的$r$，$A$的任意$r$列都是线性独立的。

上述理论描述为：

假定$y = Ax_0$，而且有$\Vert x_0\Vert_0 \leq \frac{1}{2} krank (A)$，那么$x_0$也是唯一下面最小化问题的唯一最优解： \[ \text{minimize }\Vert x\Vert_0\\ \text{subject to } Ax = y \] ### Projected Subgradient Decent for $l^1$ minimization

对于$l^1$的最小化的解决实际上与我们经常遇到的$l^2$范数是有较大区别的。现在有下面这样的最小化问题： \[ \text{minimize } \Vert x\Vert _1\\ \text{subject to } Ax = y \] 上面的问题有两个需要解决的困难：

nontrivial constraints(非平凡约束)：需要满足$Ax = y$.
nondifferentiable objective(不可导的目标函数)。$l^1$问题不是可导函数，局部会出现不可导的情况。下面对这两个问题一一进行分析解决。

Constraints

解决Constraints的最简单的方法是使用投影梯度。所有满足约束的向量，构成一个子空间(subspace)，我们计算出来的梯度可以投影到这个子空间上，利用投影之后的梯度来进行梯度下降，就是投影梯度下降的思想。一般来说，带有约束的优化问题可以写成下面的形式： \[ \text{minimize } f(x)\\ \text{subject to } x \in C \] 其中$C$是一个约束集合，一般的梯度下降算法迭代步骤为： \[ x_{k+1} = x_k - t_k\nabla f(x_k) \] 而投影梯度算法就是将结果$x_{k+1}$投影到$C$上。一个点$z$在集合$C$上的投影也就是集合上距离$z$最近的点，定义为： \[ \mathcal{P}_{C}[\boldsymbol{z}]=\arg \min _{\boldsymbol{x} \in C} \frac{1}{2}\|\boldsymbol{z}-\boldsymbol{x}\|_{2}^{2} \equiv h(\boldsymbol{x}) \] 对于一般的$C$，投影可能不存在或者不唯一，但是对于凸集合来说，投影是很好的被定义了，而且有很多有用的性质。如果$A$是行满秩的，那么集合$C = \{x|Ax = y\}$上的投影有一个非常简单的形式： \[ \mathcal{P}_{ \{\boldsymbol{x} | \boldsymbol{A} \boldsymbol{x}=\boldsymbol{y} \} }[\boldsymbol{z}]=\boldsymbol{z}-\boldsymbol{A}^{T}\left(\boldsymbol{A} \boldsymbol{A}^{T}\right)^{-1}[\boldsymbol{A} \boldsymbol{z}-\boldsymbol{y}]. \] 有兴趣了可以尝试推导一下上式的计算过程。

Nondifferentiability

对于不可导问题，因为我们优化的问题虽然不可导，但是依然是凸函数，因此我们可以使用次梯度。这里简单说一下什么是次梯度，实际上一张图就可以看明白了：

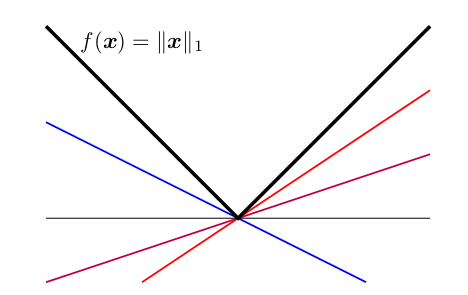
从几何的角度上来说，我们希望梯度提供一个迭代的方向，但是由于不可导，梯度并不存在，但是实际上很多方向都可以作为迭代方向的估计，如上图中，红线的斜率就是次梯度。

对于凸函数，次梯度$c$需要满足： \[ f(x) - f(x_0) \geq c(x - x_0) \] 可以看到次梯度一般不是唯一的而是一个区间，实际上我们对不可导的点左右求极限： \[ \begin{aligned} a &=\lim _{x \rightarrow x_{0}^{-} } \frac{f(x)-f\left(x_{0}\right)}{x-x_{0} } \\ b &=\lim _{x \rightarrow x_{0}^{+} } \frac{f(x)-f\left(x_{0}\right)}{x-x_{0} } \end{aligned}\\ a \leq b \] 那么处于$[a,b]$之间的都可以称为次梯度。

对于次梯度更严格的定义如下：
$f: \mathbb R ^n \rightarrow \mathbb R$是一个凸函数。那么$f$在$x_0$点的次梯度为满足下式的任意$u$： \[ f(\boldsymbol{x}) \geq f\left(\boldsymbol{x}_{0}\right)+\left\langle\boldsymbol{u}, \boldsymbol{x}-\boldsymbol{x}_{0}\right\rangle, \quad \forall \boldsymbol{x}. \] 而次导数是在该点所有次梯度的集合： \[ \partial f\left(\boldsymbol{x}_{0}\right)=\left\{\boldsymbol{u} | \forall \boldsymbol{x} \in \mathbb{R}^{n}, f(\boldsymbol{x}) \geq f\left(\boldsymbol{x}_{0}\right)+\left\langle\boldsymbol{u}, \boldsymbol{x}-\boldsymbol{x}_{0}\right\rangle\right\}. \] 因此对于次梯度下降，迭代步骤为： \[ \boldsymbol{x}_{k+1}=\boldsymbol{x}_{k}-t_{k} \boldsymbol{g}_{k}, \boldsymbol{g}_{k} \in \partial f\left(\boldsymbol{x}_{k}\right). \] 截止到这里，我们就可以推导出次梯度下降算法了： \[ \boldsymbol{x}_{k+1}=\mathcal{P}_{\mathcal{C} }\left[\boldsymbol{x}_{k}-t_{k} \boldsymbol{g}_{k}\right], \quad \boldsymbol{g}_{k} \in \partial f\left(\boldsymbol{x}_{k}\right) \] 由于次梯度是无穷多个的，对于一维的变量，$\vert x\vert$在$x=0$的次梯度为区间$[-1,1]$的任何一个数字都可以，也就是：(x) ＝[-1,1].

我们用$(x) $来表示次导数。对于多维向量，有下面的引理： **Lemma**: 现在有$xR^n$, $I = \text{supp}(x)$，那么： \[ \partial\|\cdot\|_{1}(\boldsymbol{x})=\left\{\boldsymbol{v} \in \mathbb{R}^{n} | \boldsymbol{P}_{I} \boldsymbol{v}=\operatorname{sign}(\boldsymbol{x}),\|\boldsymbol{v}\|_{\infty} \leq 1\right\} \] 这里，$\boldsymbol{P}_{I} \in \mathbb{R}^{n \times n}$是坐标$I$的正交投影： \[ \left[\boldsymbol{P}_{I} \boldsymbol{v}\right](j)=\left\{\begin{array}{ll}{\boldsymbol{v}_{j} } & {j \in I} \\ {0} & {j \notin I}\end{array}\right. \] 证明这里就不赘述了。

到了这里我们可以总结出次梯度下降算法，用来解决$l^1$的minimization(注：下图中$A^* = A^T$，表示转置):

Exprimental Result

都说用$l^1$来解决稀疏解是相对有效的方法，因此在这里类似于$l^0$，做了一个实验，看$l^1$对恢复稀疏向量上表现如何。我们知道在$l^0$的情况下，只要满足一定条件它一定能恢复原来的稀疏向量。使用同样的方法设计实验，维度是$200\times 500$，非零entry个数$k$从0到500，算法使用上述提到的投影次梯度下降。这其中，首先随机生成$A,x$，根据$y=Ax$得到$y$，再试图用上述算法去恢复$x$。由于数值精度问题，计算机中完全等于0是比较困难一件事，因此设定一个阈值，只要小于该阈值就视为零。算法的代码如下：

# A implementation of Projected Subgradient Decent
# created by Guoqing Zhang 2019.7.14

import numpy as np
from numpy.linalg import inv
import datetime
import matplotlib.pyplot as plt
# Use T and tildeX to compute projection
def computeProjection(A,y):
    I = np.identity(A.shape[1])
    I = np.mat(I)
    A = np.mat(A)
    y = np.mat(y)
    temp =  A.transpose() *inv(A * A.transpose())
    T = I -temp*A
    tildeX = temp*y
    return [T,tildeX]
def randomSequenceNoRepeat(k,n):
    r = list(range(0,n))
    
    for i in range(k):
        j = np.random.random_integers(0,n-1)
        #print(j)
        r[i],r[j] = r[j],r[i]
    return r[:k]
# k means the sparsity, m, n is the dimension of matrix A
def randomGeneratexAy(k,m,n):
    A =  np.random.randn(m,n)
    x = np.random.rand(n)
    A = np.mat(A)
    x = np.mat(x).transpose()
    zero_indice = randomSequenceNoRepeat(n-k,n)
    for i in zero_indice:
        x[i] = 0
    y = A*x 
    return x,A,y
# recoverX
def recoverX(A,y):
    T,tildeX = computeProjection(A,y)
    x = np.zeros(A.shape[1])
    x = np.mat(x).transpose()
    
    for i in range(1,10000):
        #print(i,"iteration...")
        x = tildeX + T*(x - 1/i * np.sign(x))
    return x
def drawResult(sf):
    x = list(range(0,len(sf)))
    plt.plot(x,sf)
    plt.show()

if __name__ == "__main__":
    m = 200
    n = 500
    frac = [0 for i in range(501)]
    last = 500
    for i in range(50):
        frac[i] = 1.0
    
    for k in range(50,501):
        success = 0
        for i in range(60):
            #starttime = datetime.datetime.now()
            x,A,y = randomGeneratexAy(k,m,n)
            #print(x)
            hatX = recoverX(A,y)
            hatX = hatX - x
            hatX = np.fabs(hatX)
            hatX[hatX<0.001] = 0 
            hatX[hatX!=0] = 1   
            #endtime = datetime.datetime.now()
            #print((endtime - starttime).microseconds/1000.0)
            if np.sum(hatX) == 0.0:
                success = success + 1
        frac[k] = success/60
        print(k,success/60)
        if(frac[k] == 0.0):
            last = k
            break
    for i in range(last,501):
        frac[k] = 0.0
    frac[0] = 0.0
    drawResult(frac)

最后结果如图：

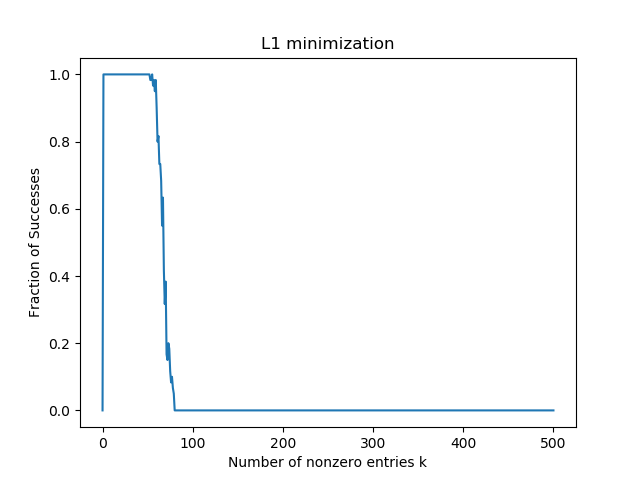
这个图不是非常的顺滑，不过有了大致的趋势，可能是迭代次数不够导致的,也不知道是不是实现的问题。一般来说这个曲线如下图：

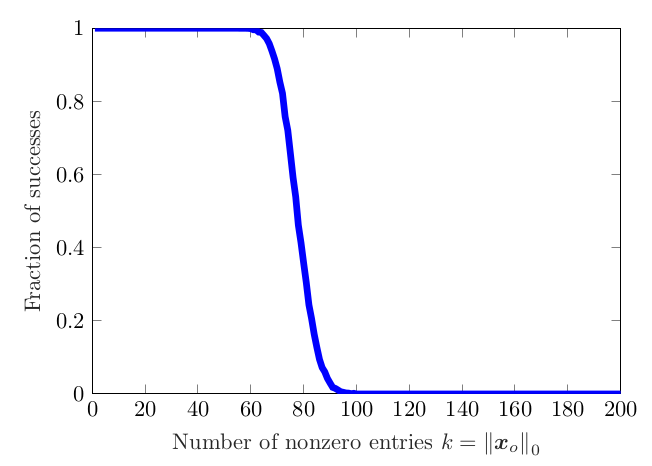
可以看到在稀疏性很大时候，$l^1$也几乎总是能恢复到原始的向量。这体现了$l^1$范数在解决稀疏问题的优越性。不过上述程序运行速度很慢，因为投影次梯度收敛速度很慢。之后会介绍更快速的优化算法。