SLAM——后端(二)Bundle Adjustment
Bundle Adjustment近些年在SLAM的研究中起到了非常重要的作用。Bundle Adjustment是将特征点与相机位姿一起作为优化变量,使得整体误差尽量变小。因为是非线性优化,不一定能找到全局最小值,因此对初始值的依赖比较大。另外,可以想象的到,BA需要计算的矩阵维度非常大,但是因为它特殊的结构,使得BA的计算简化了不少。
投影模型与BA代价函数
之前我们曾经介绍过投影模型以及畸变,现在我们重新复习下一个世界坐标系下的点\(p\)投影到照片上的过程。
- 将世界坐标系转换到相机坐标: \[ P' = Rp+t = [X',Y',Z']^T\]
- 将\(P’\)投影到归一化平面,得到归一化坐标: \[ P_c = [u_c,v_c,1]^T = [\frac{X'}{Z'},\frac{Y'}{Z'},1]\]
- 考虑径向畸变: \[ \left\{ \begin{matrix} u'_c = u_c(1+k_1r_c^2 + k_2r_c^4)\\ v'_c = v_c(1+k_1r_c^2 + k_2r_c^4) \end{matrix} \right.\]
- 根据相机内参,得到像素坐标: \[ \left\{ \begin{matrix} u_s = f_xu'_c + c_x\\ v_s = f_yv'_c+c_y \end{matrix} \right.\]
实际上,上面的一系列过程就是观测方程\(z = h(x,y)\)。具体地说,\(x\)指代的是此时相机的位姿,也就是\(R,t\),对应的李代数为\(\xi\)。而\(y\)指的是路标,也就是三维点\(p\),观测的数据是像素坐标\(z = \triangleq [u_s,v_s]^T\)。以最小二乘的角度考虑可以得到误差项: \[ e = z - h(\xi,p). \] 把其他时刻的观测量也考虑进来,设\(z_{ij}\)为位姿\(\xi_i\)下对\(p_j\)的观测数据,则整体代价函数为: \[ \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^n \Vert e_{ij}\Vert^2 = \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^n \Vert z_{ij} - h(\xi_i,p_j) \Vert^2. \] 求解上述问题,就相当于对位姿和路标同时做了调整,也就是所谓的Bundle Adjustment。
BA求解
很明显,BA问题不是一个简单的线性问题。我们把自变量定义为所有代优化的变量: \[ x = [\xi_1,\xi_2,...,\xi_m,p_1,...,p_n]^T \] 假如\(\Delta x\)是整体自变量的增量,则: \[ \frac{1}{2} \Vert f(x + \Delta x)\Vert^2 \approx \frac{1}{2} \sum_{i=1}^m\sum_{j=1}^n \Vert e_{ij}+F_{ij}\Delta \xi_{i}+E_{ij}\Delta p_j \Vert^2. \] 上式中\(F_{ij},E_{ij}\)分别为误差项对相机位姿与路标的偏导数。我们在之前的内容(PnP)中也推导过它们的形式。现在,我们把相机位姿变量放在一起: \[ x_c = [\xi_1,...,\xi_m]^T \in \mathbb{R}^{6m}, \] 同理,把空间点变量也放在一起: \[ x_p = [p_1,...,p_n]^T \in \mathbb{R}^{3n} \] 则增量误差可以写为: \[ \frac{1}{2} \Vert f(x + \Delta x)\Vert^2 \approx \frac 1 2 \Vert e+F\Delta x_c E \Delta x_p \Vert^2 \] 上式由很多小型二次项和变成了一个整体的二范数,因此这里的雅科比矩阵\(E,F\)也是对整体变量的导数,它将是一个很大的矩阵,是由不同的\(F_{ij},E_{ij}\)拼接起来的。当然,由之前的非线性优化,我们可以使用高斯牛顿或者列文伯格——马夸尔特法来进行找到极小值,但是无论使用哪个都会面对增量线性方程: \[ H \Delta x = g \] 只不过在高斯牛顿中: \[ H = J^TJ \] 列文伯格中: \[ H = J^TJ+\lambda I \] 由于我们把变量归类成为了位姿和空间点两种,所以雅科比矩阵可以分块为: \[ J = [F,E] \] 如果使用高斯牛顿法,则: \[ H = J^TJ = \begin{bmatrix} F^TF & F^TE\\ E^TF & E^TE \end{bmatrix}. \] 由于考虑了所有的优化变量,这个矩阵维度是非常大的。不过这里的\(H\)矩阵是有一定的特殊结构的,我们可以用它来加速求解过程。
稀疏性和边缘化
实际上,BA这个概念很早就提出了,不过当时研究者认为上述\(H\)矩阵太大,计算量是不可能完成的任务,直到近十年发现\(H\)矩阵的稀疏性可以加速求解。
首先,我们来考虑这个问题,就是cost function对变量\(\xi_i,p_j\)的雅科比矩阵,实际上只有\(e_{ij}\)与它有关,也就是: \[ J_{ij}(x) = \left(0_{2\times 6},...,0_{2\times 6},\frac{\partial e_{ij} }{\partial \xi_i},...,0_{2\times 3},...,0_{2\times 3},...,\frac{\partial e_{ij} }{\partial p_j},0_{2\times 3},...,0_{2 \times 3}\right). \] 上式中\(0_{2 \times 6}\)表示\(2\times 6\)的零矩阵。该误差项对于相机姿态的偏导为\(2\times 6\),对于路标点的偏导为\(2 \times 3\)(详情见PnP)。实际上这个很符合直觉,因为别的地方的误差项与当前的位姿和路标是无关的。
假如\(J_{ij}\)只在\(i,j\)处有非零块,它对于\(H\)的贡献为\(J_{ij}^TJ_{ij}\)。不难理解这个\(J_{ij}^TJ_{ij}\)也只有4个非0块,分别位于\((i,i),(i,j),(j,i),(j,j)\)。而对于\(H\): \[ H = \sum_{i,j}J_{ij}^TJ_{ij}, \] 我们将\(H\)分块: \[ H = \begin{bmatrix} H_{11}&H_{12}\\ H_{21}&H_{22} \end{bmatrix}. \] 分块的依据是,\(H_{11}\)只和相机位姿有关,而\(H_{22}\)只和路标点有关。同时还有下面的事实成立:
- \(H_{11}\)是对角阵,只在\(H_{ii}\)处有非零块
- \(H_{22}\)也是对角阵,只在\(H_{jj}\)处有非零块
- 对于\(H_{12}\)或者\(H_{21}\),它们是稠密还是稀疏是不确定的。
注意,上述对角阵针对的是分块矩阵,并不意味着是只有对角线元素非0。
这就显示了\(H\)矩阵的稀疏结构。一般情况下的\(H\)矩阵如图:
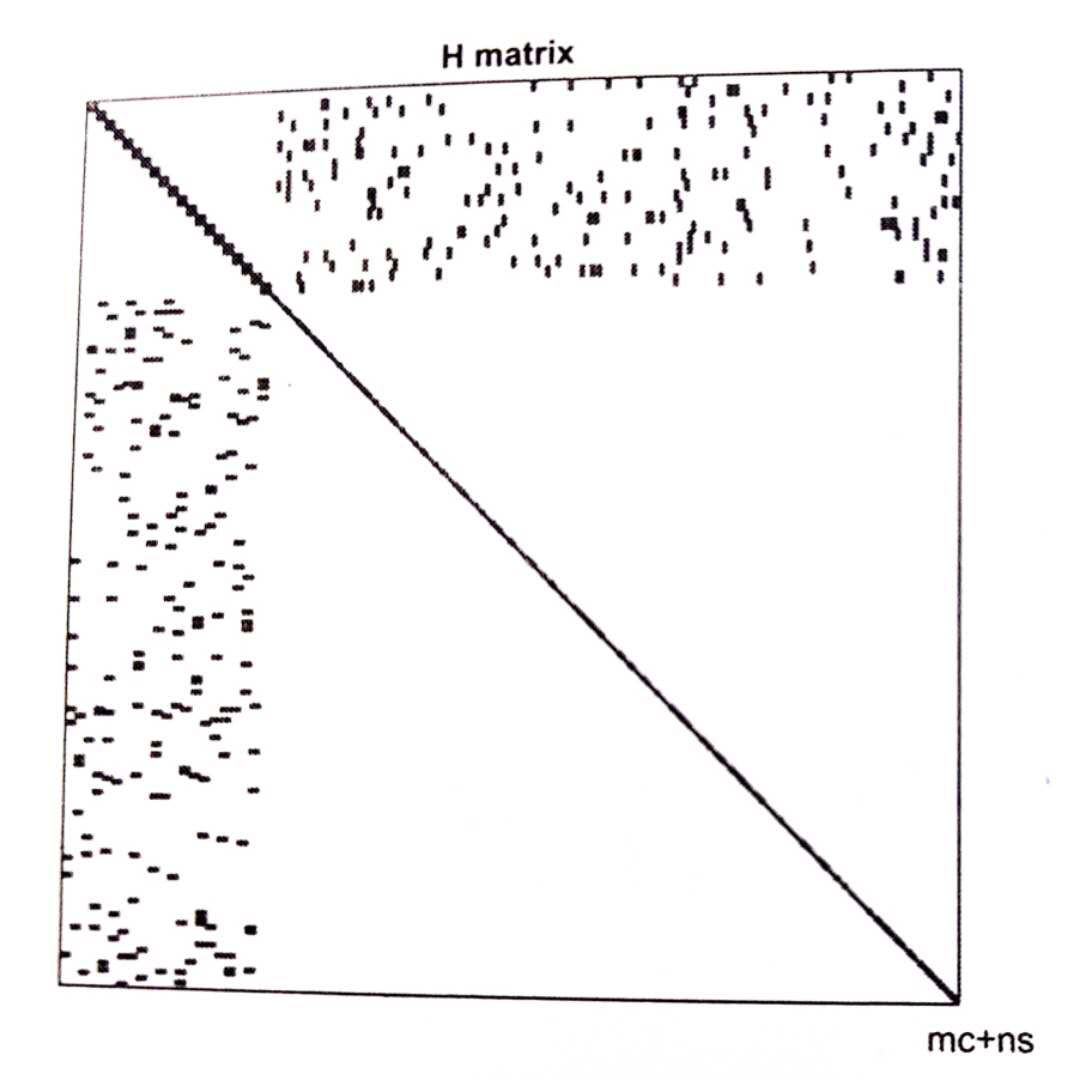
对于这种稀疏矩阵的求解,存在许多可以加速计算的方法,在这篇文章中会介绍一种叫做边缘化(marginalization)的方法。为了方便后面的说明,我们将矩阵分块为\(B,E,E^T,C\)四个块。如图:
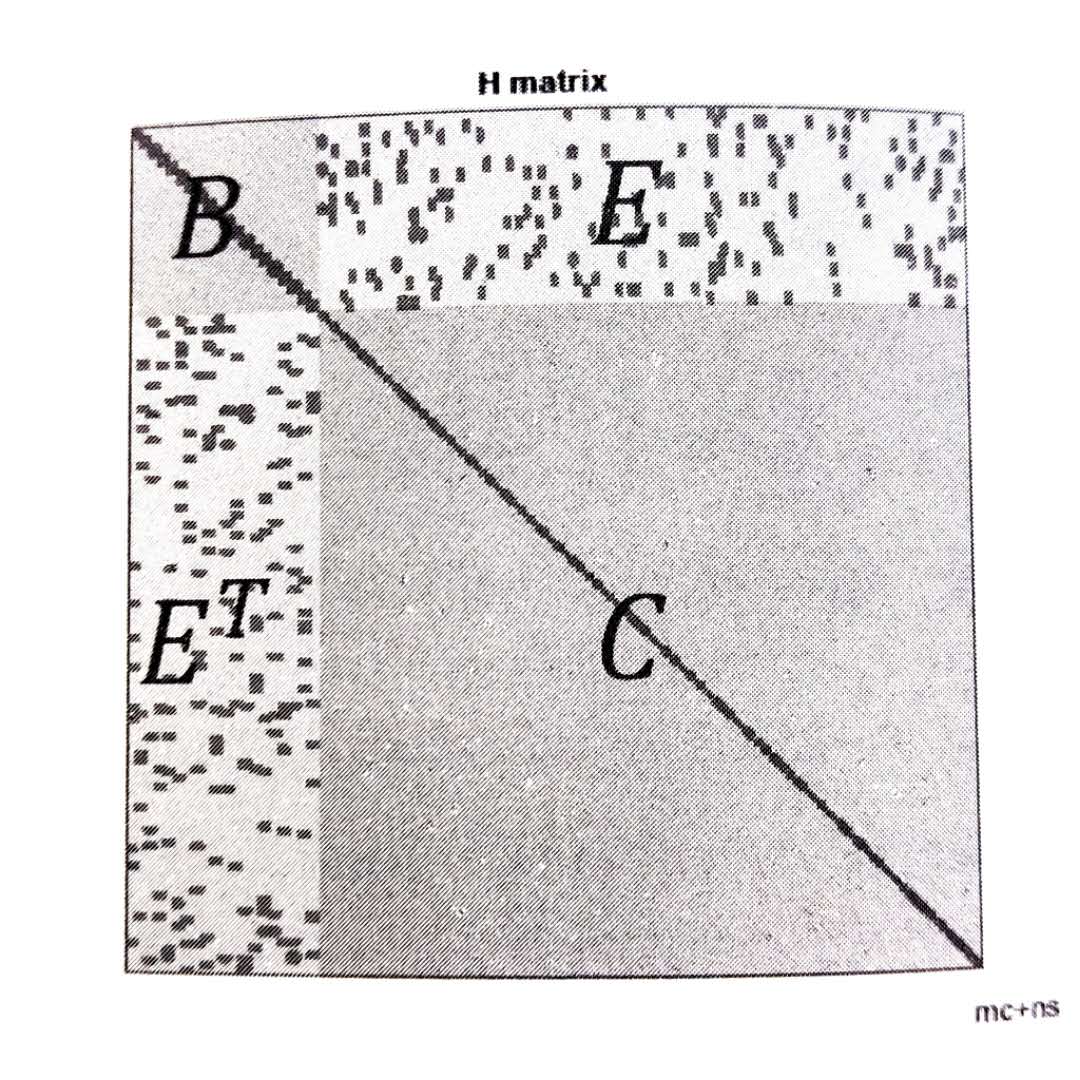
因此,对应的线性方程组\(H\Delta x = g\)可以写成下面的形式: \[ \begin{bmatrix} B&E\\ E^T&C \end{bmatrix} \begin{bmatrix} \Delta x_c\\ \Delta x_p \end{bmatrix} = \begin{bmatrix} v\\ w \end{bmatrix}. \] 由于在实际中,往往路标的个数远远大于相机位姿的个数,因此实际中\(C\)的维度也比\(B\)要大很多。\(B,C\)都是对角矩阵,而\(C\)每个非零块维度为\(3\times 3\)。对角矩阵求逆难度远小于一般矩阵的难度,因此我们只需要对对角线矩阵块分别求逆即可。考虑到这个,我们对线性方程组进行高斯消元,目的是消去\(E\): \[ \begin{bmatrix} I&-EC^{-1}\\ 0&I \end{bmatrix}\begin{bmatrix} B&E\\ E^T&C \end{bmatrix}\begin{bmatrix} \Delta x_c\\ \Delta x_p \end{bmatrix} = \begin{bmatrix} I&-EC^{-1}\\ 0&I \end{bmatrix}\begin{bmatrix} v\\ w \end{bmatrix}. \] 整理可得: \[ \begin{bmatrix} B - EC^{-1}E^T & 0\\ E^T & C \end{bmatrix}\begin{bmatrix} \Delta x_c\\ \Delta x_p \end{bmatrix} = \begin{bmatrix} v - EC^{-1}W\\ w \end{bmatrix}.\]
经过消元以后,方程第一行变成和\(\Delta x_p\)无关的项,拿出来可以得到: \[ \begin{equation} [B-EC^{-1}E^T]\Delta x_c = v - EC^{-1}w. \end{equation} \] 通过上述方程求解得到\(\Delta x_c\),代入原方程求解得到\(\Delta x_p\)。这个过程被称为Marginalization,或者Schur消元。它的优势在于利用了对角块矩阵的逆更好求,加速了求解过程。
至于方程\((1)\),它的求解没有什么特殊的办法。我们记此方程稀疏为\(S\)矩阵,它的维度和\(B\)一致。\(S\)矩阵的稀疏性是不规则的,它的物理意义为,如果在S矩阵非对角线上存在非零矩阵块,那么意味着该处对应的两个相机位姿有共同观测的路标。因此\(S\)矩阵的稀疏性主要与实际场景相关。以上就是对于\(H\)矩阵稀疏结构的应用。
从概率的角度来说,我们将对于\((\Delta x_c,\Delta x_p)\)的求解转化成了先求\(\Delta x_c\)再求\(\Delta x_p\),相当于做了条件概率的展开: \[ P(x_c,x_p) = P(x_c)\cdot P(x_p\vert x_c). \] 因此相当于求了边缘分布,所以被称为边缘化。
Robust Kernel function
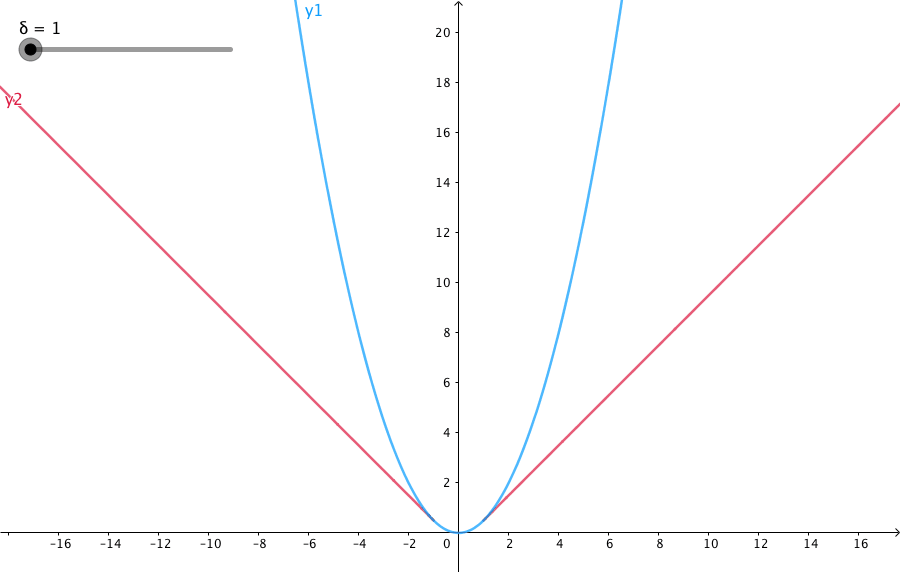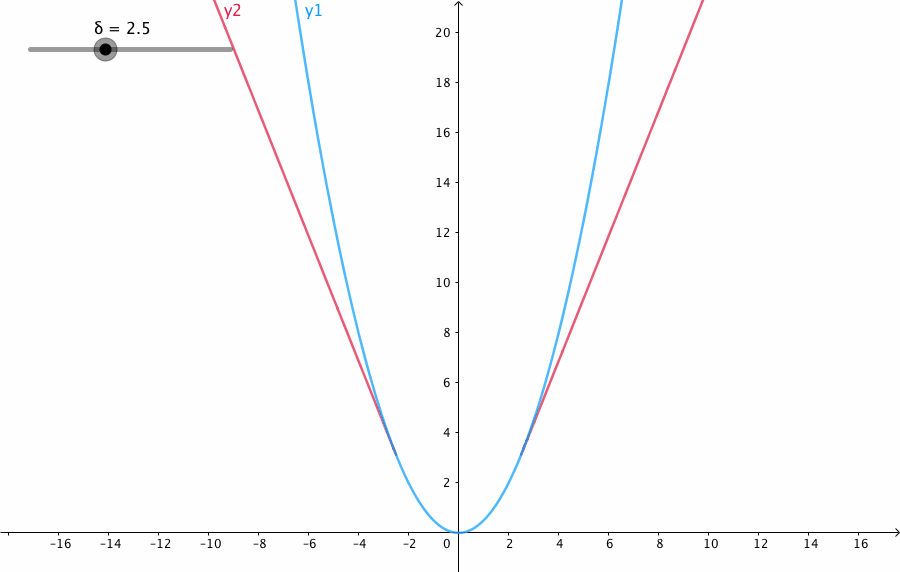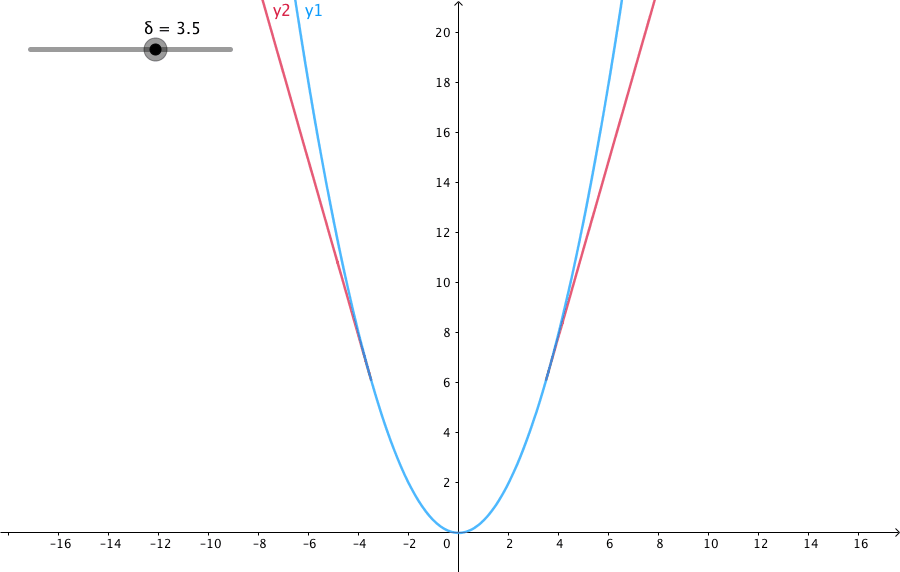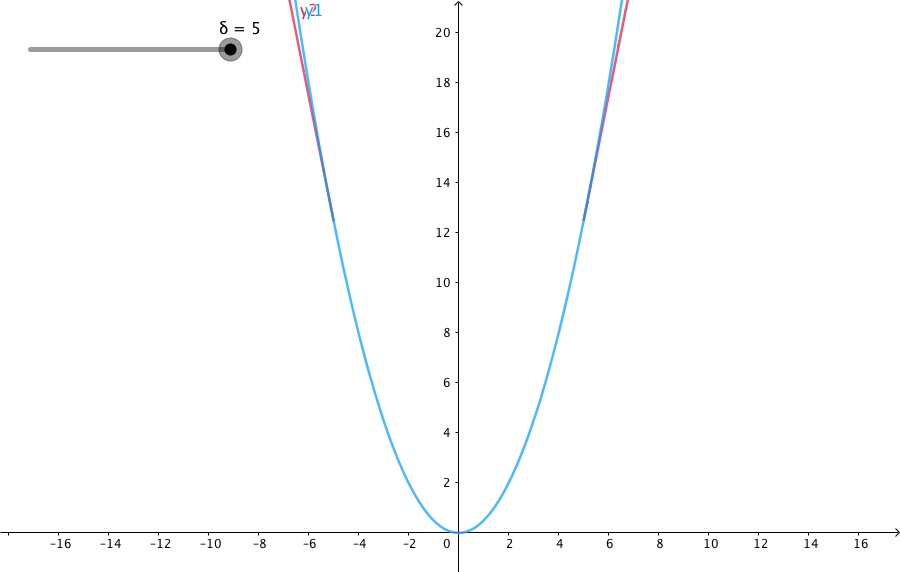
此外,我们在介绍一个鲁棒的核函数。因为我们在用二范数误差时候,假设的是特征点匹配都是正确的。而实际中,经常出现误匹配的现象。在优化时候,我们依然当成了正确的匹配,这时候为了满足这个错误项,就会朝着错误的方向去走了。其中一个原因是二范数的增长太快。因此研究者提出了一些比二范数增长更慢的核函数,用的最多的是Huber norm: \[ H(e) = \left \{\begin{matrix} \frac 1 2 e^2 & \vert e\vert \leq \sigma\\ \sigma(\vert e\vert - \frac{1}{2}\sigma) & \text{otherwise} \end{matrix} \right. \] 可以看到的是当误差大于某个阈值之后,函数增长变成了一次形式,同时还方便求导。相对于二范数度量,它有更好的鲁棒性。它的图像如下: