信息论——信息速率失真函数与熵压缩编码(一)
之前我们研究的问题,冗余度压缩编码以及信道编码(增加信息冗余度,以对抗信道中的传输错误),目的都是对信息进行可靠无差错的传输,信息熵没有变化,也就是是保熵的。之后的内容,我们不再保证信息传输是无差错的。
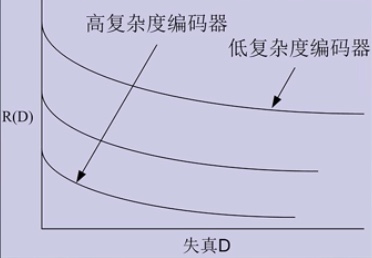
在实际中,很多情况下我们是没有必要把信息的所有内容都保留下来的。比如看视频的时候,有高清标清的选择,对应于不同的网络情况。同样的还有图片的有损压缩等等。
连续随机变量的量化
考察随机变量\(X \sim
N(0,\sigma^2)\),如果对该随机变量进行无失真编码是不可能的,假如我们需要用\(R\)比特来表示\(X\)。所以被表示的结果\(\hat X\)相对于原来的\(X\)一定是有失真的。而这个失真如何度量呢?最简单的方法是采用平方误差度量最小化:
\[
E(x - \hat X(x))^2 = \int_{-\infty}^{\infty} (x - \hat X(x))^2 p(x)dx.
\] 现在假设\(R=1\),比较显然的是该符号应该代表X的正负。为了最小化误差,恢复值应该为其代表区域的条件平均:
\[
\hat X(x) = \left \{ \begin{matrix} \sqrt{\frac{2}{\pi} }\sigma
&\hat x = 1(x\ge 0)\\ -\sqrt{\frac{2}{\pi} }\sigma & \hat x=0(x
< 0) \end{matrix} \right .
\] 这个值是如何求得的?
首先我们要理解上面话的意思,最小化误差,其实也就是X的期望。对于整个分布来说,\(X\)的期望当然是0,现在我们只看左侧,希望能得到左侧的条件分布X的期望是多少。
\[
\begin{aligned} E(X) &= \int_{-\infty}^0 xf(x)dx\\
&=\int_{-\infty}^0 2\sigma^2\cdot\frac{1}{\sigma \sqrt{2\pi}
}exp(-\frac{x^2}{2\sigma^2}) f(x) d\frac{x^2}{2\sigma^2}\\ &=
-\frac{2\sigma}{\sqrt{2\pi} } exp
(-\frac{x^2}{2\sigma^2})|_{-\infty}^{0}\\
&=-\frac{2\sigma}{\sqrt{2\pi} } = -\sqrt{\frac{2}{\pi} }\sigma
\end{aligned}
\] 如果\(R >
1\),又如何划分量化区间?如何选取这个\(2^R\)个\(\hat
X(x)\)的取值?这个问题就没有上面那么简单了。
针对随机变量的最优(最小失真)量化准则:
- 如果给定了一组\(\hat X(x)\),那么将随机变量\(x\)映射到最近的\(\hat X(x)\)可以最小化量化失真。由这种映射形成的划分称为Voronoi(Dirichlet)划分。
- \(\hat X(x)\)的选取可以最小化对应趋于中的条件预期失真。
率失真理论的基本概念
失真度量(失真函数)是这样一个映射: \[ d:X \times \hat X \rightarrow R^{+} \] 它将源字母-恢复字母对映射到一个非负的实数,来代表失真多少。当原始字母集与映射的字母集是离散的,可以用一个矩阵来表示失真的大小,而在连续的情况下,这就是一个函数。失真函数永远都是非负的,因为我们没有办法说一个失真是负的。如果失真是有限的,则函数为有界函数。
下面举两个失真度量的例子:
- 离散对称信源,信道输入输出及失真函数为: \[X = {x_1,...,x_k}\\ \hat X = { x_1 ,...,\ x_k}\\ d(x_i,x_j) = \left \{\begin{matrix} 0 & i=j\\ 1 & i \ne j \end{matrix} \right.\]
当恢复符号与发送符号对应时,失真不存在,不对应时,失真为1。这个失真被称为汉明失真。汉明距离在ORB特征匹配中是非常有用的。该失真矩阵为:
\[
[d] = \begin{bmatrix} 0&1&\cdots&1\\
1&0&\cdots&1\\ \vdots&\vdots&\ddots&\vdots\\
1&1&\cdots&0 \end{bmatrix}
\] * 连续信源,平方失真度量:\(d(x,\hat
x) = (x - \hat x)^2\)
在语音编码中,常用的失真度量为:Itakura-Saito距离。而在图像处理中,目前还没有统一的失真度量,常用的还是平方失真度量。
因此,失真度量的选择要与实际结合。
平均失真
失真函数在输入输出联合空间中取统计平均为 \[ D \triangleq \sum_{x_i,\hat x_j} p(x_i)q(\hat x_j | x_i)d(x_i,\hat x_j) \triangleq E[d(X,\hat X)] \] 在给定信源分布与转移概率分布时,上式为信道传输失真总体的平均度量。
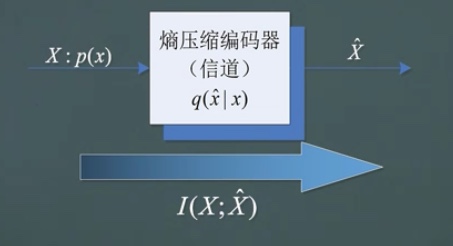
现在我们想做的事情如下图,\(X\)经过信道之后,得到\(\hat X\),我们希望\(I(X;\hat X)\)尽可能小,以此来压缩比特的传输。当然,这个互信息是不能为0的,那一切就失去了意义。压缩下有个前提,就是对失真函数的约束。
率失真函数
针对信源\(X\)和失真度量\(d(x,\hat x)\),信息的率失真函数\(R^{(I)}(D)\)定义为: \[ R^{(I)}(D) = \min_{q(\hat x|x):\sum_{x,\hat x} p(x)q(\hat x|x )d(x,\hat x) \leq D} I(X;\hat X) \] 这就是信息论意义下的率失真函数的定义,而\(R\)的上标\((I)\)标识了这一点。
注:我们无法操作信源,能做的是最小化针对所有可能的条件分布\(q(\hat x | x)\),并且使得联合分布满足要求的失真约束。这个函数求得的最小值,并不一定是可操作得到的,只是数学上的一个最小值。
率失真编码
率失真编码\((2^{nR},n)\)包括一个编码函数 \[ f_n:X^n \rightarrow \{1,2,...,2^{nR} \} \] 一个解码函数: \[ g_n:\{1,2,...,2^{nR} \} \rightarrow X^n \] 以及一个与\((2^{nR},n)\)相关的失真: \[ E[d(X^n,g_n(f_n(X^n)))] = \sum_{x^n} p(x^n)d(x^n,g_n(f_n(x^n))) \] 注:
\(g_n(1),g_n(2),…,g_n(2^{nR})\)构成了一个码本,以\(\hat X^n(1),…,\hat X^n(2^{nR})\)表示
\(f^{-1}_n(1),…,f^{-1}_n(2^{nR})\),也就是f的反函数为对应的量化区间。
率失真区域
如果存在一组率失真编码\((2^{nR},n)\),使得\(\lim_{n \rightarrow \infty} E[d(X^n,g_n(f_n(X^n)))] \leq D\),则称率失真对\((R,D)\)是可达的。
信源的率失真区域是对所有可行率失真对\((R,D)\)的闭包。
给定失真度量约束\(D\),率失真函数\(R(D)\)是速率\(R\)跑遍率失真区域获得的下确界。
这个率失真函数是实际可以实现的。而香农告诉我们(香农第三定理),这两个率失真函数的值是相等的。
率失真定理(香农第三定理)
给定具有独立同分布\(p(x)\)的信源X和有界的失真度量\(d(x,\hat x)\),率失真函数等于信息的率失真函数,即: \[ R(D) = R^{(I)}(D) = \min_{q(\hat x|x):\sum_{x,\hat x} p(x)q(\hat x|x )d(x,\hat x) \leq D} I(X;\hat X) \] 是在失真约束\(D\)下可以获得的最小信息传输速率。
\(R^{(I)}(D)\)的性质
直接思维中\(R(D)\)的形式:
单调减函数
\(R^{(1)}(D)\)是非增函数。这个不难理解,证明如下:
如果\(D_2 \ge D_1\),则: \[ {q(\hat x| x), E[d(x,\hat x)] \leq D_1} \subset {q(\hat x| x), E[d(x,\hat x)] \leq D_2} \] 由于在子集上取得的最小值不可能比全集更小,因此可以得到: \[ \min\{I(X;\hat X):E[d(x,hat x)] \leq D_2\} \leq \min\{I(X;\hat X):E[d(x,hat x)] \leq D_1\} \] 从而得到:\(R(D_2) \leq R(D_1)\)。
定义域
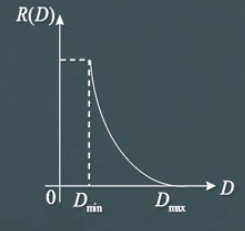
\(R^{(I)}(D)\)的定义域是\((D_{min},\infty)\),且存在\(D_{max}\),当\(D \ge D_{max}\)时,\(R^{(I)}(D) = 0\)。
这个在直觉上也是很好理解的。平均失真D是非负实函数\(d(x,\hat x)\)的期望,下限为0,则允许失真D的下限也为0,对应于不允许失真的情况。
当信源\(p(x)\)给定时,失真取决于转移矩阵\(q(\hat x|x)\)的取值。因此\(D\)是有一个最小值的。
如果允许失真大到一定值,错得太离谱,可以不用传输了,这时候就得到\(R^{(I)}(D)=0\)。
下面是一个关于\(D_{min}\)的例子:
下凸性质
\(R(D)\)是\(D\)的下凸函数。下面是一个简单的证明:
由于输入分布\(p(x)\)已知,所以输入与输出的互信息仅与转移概率矩阵\(Q=q(\hat x|x)\)决定,记为\(I(Q)\)。设\(Q_1\)是达到\(R(D_1)\)时的转移概率矩阵,\(Q_2\)是达到\(R(D_2)\)的转移概率矩阵。定义\(Q\)是达到\(R(D)\)的转移概率矩阵,\(D = \lambda_1D_1 + \lambda_2D_2\)。
注意到:\(I(Q_1) = R(D_1)\),\(E[d(x,\hat x)] \leq D_1\),同理得到:\(I(Q_2) = R(D_2)\),\(E[d(x,\hat x)] \leq D_2\)。
在转移概率矩阵Q下,编码器的平均失真为: \[ E[d(x,\hat x)]|_Q = \lambda_1 E[d(x,\hat x)]|_{Q_1} + \lambda_2 E[d(x,\hat x)] |_{Q_2} \leq \lambda_1 D_1 + \lambda_2 D_2 = D. \] 因此,\(Q\)在可行区域中,\(R(D) \leq I(Q)\)。而互信息相对于转移概率矩阵Q是下凸函数,因此: \[ R(D)\leq I(Q) \leq \lambda_1 I(Q_1) + \lambda_2 I(Q_2) = \lambda_1 R(D_1) + \lambda_2 R(D_2) \] 由上面的性质,我们可以大约得到\(R(D)\)的图像:
率失真函数的计算
伯努利信源的率失真函数
下面是一个伯努利分布\(X\sim
Bern(p)\)的信源的传输。
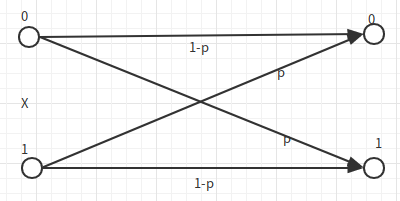
我们希望求的是: \[ R(D) = \min_{q(\hat x|x):\sum_{x,\hat x} p(x)q(\hat x|x )d(x,\hat x) \leq D} I(X;\hat X) \] 但是我们并不用按照拉格朗日等那样一般的数学方法去求得这个最小值。我们可以缩放这个\(I(\hat X;X)\),最后再证明这个等号是可以取得的。 \[ \begin{aligned} I(X;\hat X) &= H(X) - H(X|\hat X)\\ &= H(p) - H(X \oplus \hat X |\hat X )\\ &\ge H(p) - H(X \oplus \hat X) \\ &= H(p) - H(P_e)\\ & = H(p) - H(D) \end{aligned}\\ \text{where }D \leq \frac 1 2 \] 我们可以构造这样的信道,最后得到这个等号是可以取到的。如下图:
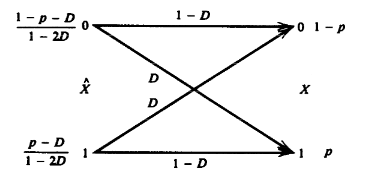
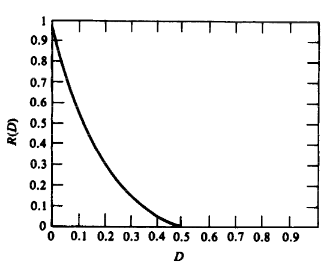
在汉明失真度量下,伯努利信源的率失真函数为: \[ R(D) = \left \{\begin{matrix} H(p) - H(D),&0\leq D\leq \min\{p,1-p\}\\ 0, & D> \min\{p,1-p\} \end{matrix} \right. \] 函数图像如下:
连续高斯信源的率失真函数
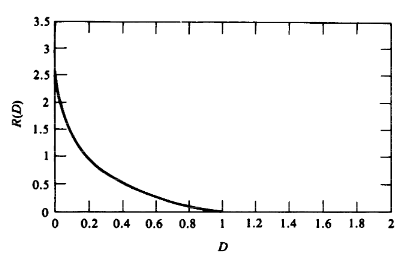
在均方失真度量下,高斯信源的率失真函数是: \[ R(D) = \left \{\begin{matrix} \frac 1 2 \log \frac{\sigma^2}{D},&0\leq D\leq \min\{p,1-p\}\\ 0, & D> \min\{p,1-p\} \end{matrix} \right. \] 图像如下:
这个证明过程和上面的伯努利情况是相似的: \[ \begin{aligned} I(X;\hat X) &= h(X) - h(X|\hat X)\\ &= \frac{1}{2} \log 2\pi e \sigma^2 - h(X - \hat X|\hat X)\\ & \ge \frac{1}{2} \log 2\pi e \sigma^2 - h(X - \hat X)\\ & \ge \frac{1}{2} \log 2\pi e \sigma^2 -h(N(0,E(X - \hat X)^2))\\ & \ge \frac{1}{2} \log 2\pi e \sigma^2 -\frac 1 2 \log 2 \pi e D\\ &= \frac 1 2 \log \frac{\sigma^2}{D} \end{aligned} \] 为了取到这个等号,我们构造的反向信道如下:
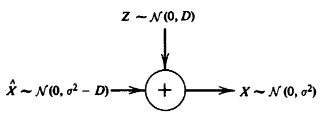
注:
- 可以将\(R(D)\)写成\(D(R) = \sigma^2 2^{-2R}\)
- 每比特失真为\(0.25\sigma^2\)
- 不等式关系:若\(X_1,X_2\)独立,\(I(X_1,X_2;Y) \ge I(X_1;Y)+I(X_2;Y)\)(Why?)
之前我们使用1bit量化标准高斯分布的连续随机变量时,量化误差为:\(\frac{\pi - 2}{\pi}\sigma^2 = 0.363\sigma^2\),也就是我们直觉中的最小和理论还有一定的差距。
恢复点: \[ \hat X(x) = \left \{ \begin{matrix} \sqrt{\frac{2}{\pi} }\sigma &\hat x = 1(x\ge 0)\\ -\sqrt{\frac{2}{\pi} }\sigma & \hat x=0(x < 0) \end{matrix} \right . \] 平均失真为: \[ D = \int_{-\infty}^{\infty}(x - \hat X(x))^2p(x)dx = \frac{\pi - 2}{\pi}\sigma^2 \] 这是为什么呢?之后我们会证明,这个最优值要在考虑足够的分组长度的情况下才能实现。