信息论——信道及其容量

Posted on Edited on In

这次来介绍信道以及信道的容量。 ## 信道容量的定义以及性质 ## ### 通信是什么? ### 物理实体A的作用引发了物理实体B的状态变化，如果A与B的变化存在一致性，我们称AB通信成功。从信息角度来看，也就是比特流端到端的无差错复制。 ### 信道的分类 ###

按照输入输出的形式以及时间取值来划分

取值 时间 信道分类
离散 离散 离散信道，数字信道
连续 离散 连续信道
连续 连续 模拟信道
离散 连续 ——

按照信道随机过程的特点分类

离散信道可以表示为n阶转移概率矩阵 \[ Q_{t_1t_2...t_n} = \left \{ q(y_{t_1t_2...t_n} | x_{t_1t_2...t_n}) \right\} \] * 无记忆信道 \[ q(y_{t_1t_2...t_n} | x_{t_1t_2...t_n}) = \prod_{i=1}^nq(y_i|x_i) \]

无记忆信道不代表输出的符号不相关，这个和输入有关。 * 平稳信道： \[ q(y_i|x_i) = q(y|x) \]

DMC(Discrete Memoryless Channel)

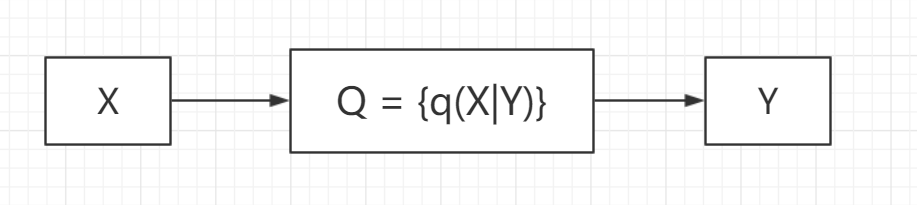\[ \begin{align} I(X^n;Y^n) = H(Y^n) - H(Y^n|X^n) \end{align} \] \[ \begin{aligned} H(Y^n)&= H(Y_1) +H(Y_2|Y_1) +...+ H(Y_n|Y_1...Y_{n-1})\\ &\leq \sum_{i=1}^n H(Y_i) \end{aligned} \] \[ \begin{aligned} H(Y^n|X^n)&= -\mathbb{E}_{XY}\log q(y^n|x^n) \\ &= -\mathbb{E}_{XY}\log \prod_{i=1}^nq(y_1|x_1)\\ &= - \mathbb{E}_{XY}\sum_{i=1}^n\log q(y_i|x_i)\\ &= -\sum_{i=1}^n \mathbb{E}_{XY}\log q(y_i|x_i)\\ &= \sum_{i=1}^n H(Y_i|X_i) \end{aligned} \]

综上我们得到： \[ I(X^n;Y^n) \leq \sum_{i=1}^nI(X_i;Y_i) \]

这让我们想到，对一个序列的输入输出互信息，我们可以试图通过处理单个时刻的输入，然后让等号取得，也就得到序列输入输出互信息的最大值。

为了让上面的等号取得，实际是比较简单，也就是当\(Y_i\)之间互相独立。下面我们来研究如何让单字母互信息得到最大值。 ### 信道容量定义 ### 对于离散无记忆信道，信道容量为： \[ C = \max_{p(x)}I(X;Y) = \max_{p(x)}I(p,Q) \]

当一个信道确定时，\(Q\)也就确定了，因此我们要做的就是调整输入字母的分布，让这个信道输入输出互信息得到最大，也就得到了信道的容量。之前介绍互信息的时候介绍了\(I(p;Q)\)这种形式，就是为了方便信道的解释。

离散无记忆信道的容量

现在来看一看最简单的信道：离散无记忆信道的容量应如何计算。这一小节主要通过举几个例子，然后再得到普遍的结论。 #### 无噪声二元信道 ####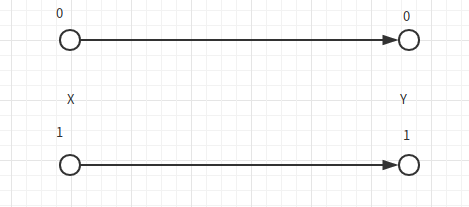

输入X，输出Y。由于传输误差错，所以每次传输都传递了1 bit的无差错信息。所以直观来说信道容量为1 bit.

利用信道容量的定义来计算，则： \[ C=\max I(X;Y) = \max(H(X) - H(X|Y)) = \max H(X) = 1\\ p(X) = (0.5,0.5) \] 如果字符个数变成m个，则这个信道容量变为：\(\log m\). #### 输出不重叠的噪声信道 ####

观察上图，我们发现这个信道有下面几个特点： 1. 信道存在噪声，输出不确定 2. 但是不确定性不影响正确估计输入 3. 信道实际是无差错的 4. X到Y是一对多映射 \[ C = \max I(X;Y) = \max(H(X)-H(X|Y)) = \max(H(X))=1\\ p(X) = (0.5,0.5) \]

因此可以看到即时有噪声，我们依然可以得到无差错的信道传输。

混乱打字机

混乱打字机把每个字母以0.5的概率映射为其自身或者下一个字母。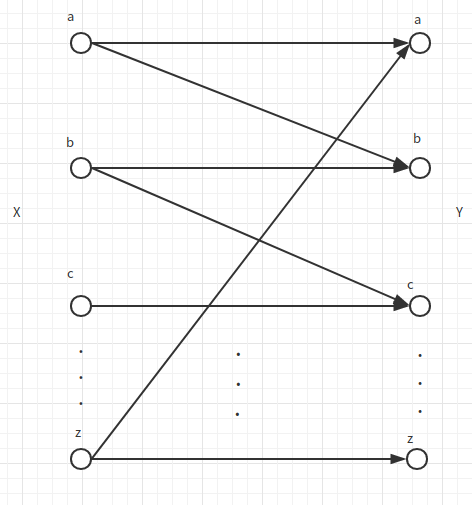

则： \[ \begin{aligned} C &= \max I(X;Y)\\ &= \max(H(Y) - H(Y|X))\\ &= \max(H(Y)-1)\\ &= \log 26 - 1 = \log 13 \end{aligned} \]

我们只是在互信息求得这个，但是我们不一定能找到一个实际的概率控制得到这个容量。而实际上，这个容量是可以达到的。

我们要求输入端只能输入\(A,C,E...\)这些字母，从而退化成了一个输出不重叠噪声信道，这称为无重叠约化。通过这个方法，我们实现了\(\log13\)的容量。实际上香农告诉我们，任何一种混乱的信道，都可以看作是混乱打字机信道。

BSC(Binary Symmetric Channel)

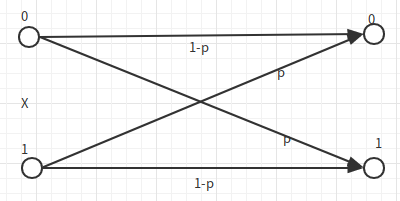
\[ \begin{aligned} C &= \max_{p(x)} I(X;Y)\\ &=\max( H(Y) - H(Y|X))\\ &=\max(H(Y) - H(p))\\ &=1-H(p) \end{aligned} \]

我们必须证明这个容量可以取到,也就是一个上确界，这样得到信道的容量才有意义。为了让\(H(Y)\)最大，那么\(p(Y)=(0.5,0.5)\),可以简单的发现这时候\(p(X) = (0.5,0.5)\).也就是我们可以通过调制信源的输入概率分布得到这个最大的容量 因此\(C_{BSC} = 1 - H(p)\)

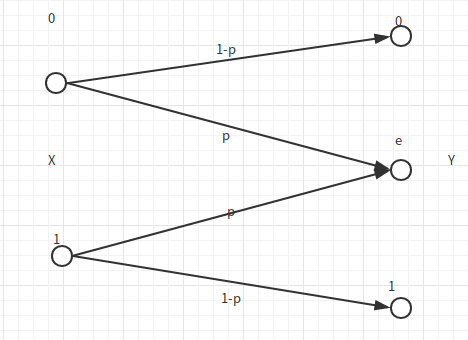
EC(删除信道)

\[ C = \max_{p(x)}I(X;Y) \] \[ \begin{aligned} I(X;Y) &= H(Y) - H(Y|X)\\ &=H(Y) - H(p)\\ &\leq \log 3 - H(p) \end{aligned} \]

这时候我们就遇到问题了，我们不能通过调制信源的输入概率分布使得\(p(Y)=(\frac{1}{3},\frac{1}{3},\frac 1 3)\)，因此上面得到的不是信道容量。因此重新计算这个容量,假设\(p(X) = (\pi,1-\pi)\)： \[ \begin{aligned} I(X;Y) &= H(Y) - H(p)\\ &= H((\pi(1-p),p,(1-\pi)(1-p)))\\ &= (1-p)H(\pi) + H(p) - H(p)\\ &= (1-p)H(\pi) \end{aligned} \]

上式中用到了熵的可加性。这时候我们可以取到\(H(\pi)=1\)，因此得到\(C = 1-p\).

离散无记忆对称信道容量

实际上，上面的几个信道有很多都属于离散无记忆对称信道。他们的特点是概率转移矩阵\(Q\)为对称矩阵，使得\(H(Y|X)\)可以由信道性质确定，大大简化了我们要思考的问题。

离散无记忆对称信道的定义： 若信道的概率转移矩阵的行互为置换，列互为置换，则该信道对称，如果行互为置换，各列之和相等，则该信道弱对称。

强对称： \[ \begin{bmatrix} \frac 1 2&\frac 1 3& \frac 1 6\\ \frac 1 6&\frac 1 2&\frac 1 3\\ \frac 1 3&\frac 1 6&\frac 1 2 \end{bmatrix} \]

弱对称： \[ \begin{bmatrix} \frac 1 3 & \frac 1 6 &\frac 1 2\\ \frac 1 3 & \frac 1 2 & \frac 1 6 \end{bmatrix} \]

不管是强对称还是弱对称，他们都有一个好处，那就是\(H(Y|X)\)不会随着信源的概率分布而改变，是一个常数。

弱对称信道Q的容量为：\(C=\log \vert Y\vert - H(Q的行向量对应的分布)\),容量在输入为等概分布时候取得。

而EC不是一个对称信道： \[ Q = \begin{bmatrix} 1-p & p & 0\\ 0 & p & 1-p \end{bmatrix} \]

一般离散无记忆信道的容量

由于\(I(p,Q)\)是\(p\)的上凸函数，因此求信道容量实际上可以表述为一个约束的极值问题： \[ \max _{p} I(p,Q)\\ s.t. \sum_{x}p(x)=1;p(x)\ge 0 \]

kkt condition

设\(f(x)\)为定义在Ｎ维无穷凸集\(S\), \(S=\{x = \(x_1,x_2,...,x_N\):x_i \ge 0,i=1,...,N\}\)上的可微上凸函数，设\(x^\* = {x_1^\*,...,x_N^\*} \in S\)，则\(f(x)\)在\(x = x^\*\)达到\(S\)上的极大值的充要条件为： \[ \frac{\partial f(x)}{\partial x_n}\lvert_{x = x^*} = 0,x_n^* > 0\\ \frac{\partial f(x)}{\partial x_n}\lvert_{x = x^*} \leq 0, x_n^* = 0 \]

我们称\(x^\*(x^\*=(x_1^\*,...,x_N^\*),x_n^\* > 0)\)为\(S\)的内点，而\(\exists x_n^\* = 0\)时，\(x^\*\)为\(S\)的边界点。

用图像来看的话会更容易理解：

上图为：

\[\min f(x,y)=ax^2-b\log y,0< x <100,0< y <100\]

实际上的kkt条件比这个更严谨，可以参考：kkt condition

由于它是一个凸函数下的充要条件，因此只要我们找到了一个点符合KKT条件，我们就可以称他为全局极值。

由KKT条件可以得到下面的关于信道容量的定理：

对于信道矩阵为\(Q\)的离散无记忆信道，其输入分布\(p^\*\)能使互信息\(I(p,Q)\)取得最大值的充要条件是： \[ I(X=x_k;Y) = C,p^*(x_k) > 0\\ I(X=x_k;Y) \leq C,p^*(x_k)=0\\ k \in {1,2,...,K} \] 其中\(I(X=x_k;Y) = \sum_{j=1}^J q(y_j|x_k) \log \frac{q(y_j|x_k)}{p(y_j)}\),表示的是信源字母\(x_k\)传送的平均互信息。

当然我们拿到一个信道以后，不一定一定要通过这样的方法来求得信道容量，很多时候我们可以联系物理猜到最好的哪个情况。如下：

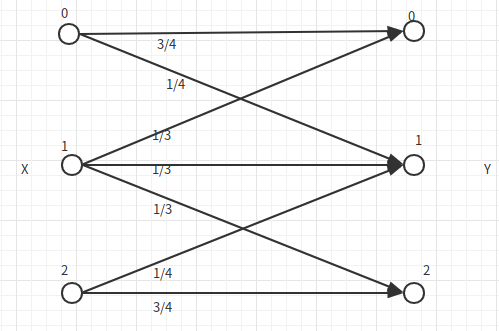
我们可以很容易看出来1是最差的情况，因为它可能映射到三种结果，而0,２一样好，因此我们猜测：\(p(x_1) = 0,p(x_2)=p(x_0)=0.5\)，计算得到： \[ I(X=x_0;Y) = I(X=x_2;Y)=0.75, I(X=x_1;Y) = 0.0251<0.75 \] 符合kkt条件，因此它的容量就是0.75. ## 信道的组合 ##

现在我们尝试将信道组合起来。 ### 级联的独立信道 ###

如上图，我们可以得到： * 由数据处理定理可以得到：\(I(Y;Z) \ge I(X;Z)\) * 随着串联信道数目的增多，整个信道容量趋近于0 * 将级联信道的\(Q_i\)乘起来，得到整个级联信道的Q，可求解级联信道的容量 * Vision：从统计的角度来看，数据处理不会带来信息增益，反而会损失信息 ### 输入并联信道 ###

这个信道的特点是，输入相同的X，输出不同的\(Y_1,Y_2,...,\)构成随机矢量Y。也就是我们将输入X同时送到N个信道中，如图：

  • 输入并联信道的容量大于任何一个单独的信道，小于\(\max H(X)\).
  • N个二元对称信道输入并联之后的信道容量，一般来说\(N\)越大，\(C_N\)越大，越接近于\(H(X)\)。
  • Vision:通信中的分集，就是典型的输入并联信道（我并不懂通信）

并用信道

并用信道的图和并联信道非常像，不过它的输入不是相同的\(X\)了，而是将\(X\)费解成了\(X_1,X_2,...,X_N\)。 * 多输入，多输出。\(X\)和\(Y\)是由比侧独立的N个信道传输 * 并用信道的容量：\(C = \sum_{n=1}^N C_n\) * Vision:通信中的复用，就是典型的并用信道

虽然并用信道的容量结论很简单，但是在实际中的操作没那么容易。我们不能简单的将信源随意划分，而是让这个划分符合各个信道容量的噪声特性，以达到最好的传输效果。

和信道

和信道和并联信道并用信道不同的是，虽然它有多个信道，但是它并不是同时使用多个，而是每次只使用一个。 * 随机应用\(N\)个信道中的一个，构成一个输入输出信道。 * 和信道的容量：\(C = \log \sum_{n=1}^N 2^{C_n}\)，信道的使用概率\(p_n(C) = 2^{C_n - C}\) * Vision: 新型通信技术——机会通信 要注意这个结论有点反直觉。我们可能会想，如果某个信道的容量大，一直使用它不就行了吗？但是这样并不会得到最大的信道容量。

举个例子，如果一个信道的转移矩阵为\(Q\): \[ Q = \begin{bmatrix} 1 - \epsilon_1&\epsilon_1&0&0\\ \epsilon_1&1 - \epsilon_1 & 0 & 0 \\ 0&0&\epsilon_2 &1 - \epsilon_2\\ 0&0&1-\epsilon_2&\epsilon_2 end{bmatrix} \]

那么这个信道的容量为多大？

如果仔细观察，可以发现这个信道实际上是一个和信道。

\[ C = \log(2^{C_1} + 2^{C_2}) \] 如果： \(\epsilon_1 = 0,C_1 = 1;\epsilon_2 = 0,C_2 = 0\);

可以发现，这两个信道一个容量为0,另一个为1,而它们的和信道容量为\(\log3>1\)。这是因为在选择使用哪个信道的时候，也包含了一定的信息。

连续信道的容量

连续信道时间依旧离散，取值是连续的。这就引发了一个问题：连续随机变量互信息非负但是不一定有限，如果输入输出相等，则此时互信息是无穷的。 这样，互信息最大值为信道容量的定义就失去了意义。 ### 容量费用函数 ### 首先说明一下，连续信道输入连续，输出连续，而信道特性不能再用一个概率转移矩阵来表示，而是一个概率密度函数。所以我们用三元组\(\{X,q(y|x),Y\}\)来表示一个连续信道。

费用函数: 设对于连续无记忆信道\(\{X,q(y|x),Y\}\)，有一个函数\(b(.)\)，对于每一个输入序列\(X = x_1x_2...x_n\)，\(b(x)>0\)。称\(b\)为\(X\)的费用。设随机矢量\(X = X_1X_2...X_n\)的联合分布为\(p(x)\)，则平均费用为： \[ \mathbb{E}[b(X)] \triangleq \sum_{x}p(x)b(x) \]

在费用约束的前提下，求输入输出互信息的最大值，得到容量费用函数： 设连续信道的\(N\)维联合输入输出分别为\(X,Y\)，则其容量－费用函数定义为： \[ C(\beta) = \lim_{N\rightarrow \infty} \frac{1}{N} \max_{p(x)}\{I(X;Y):\mathbb{E}[b(X)]\leq N \beta \} \]

连续无记忆加性噪声信道的容量

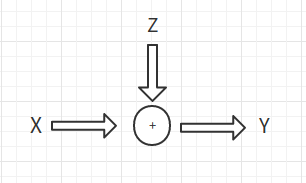
这里我们来看一个最简单的连续信道的容量费用函数。这个信道为加性噪声信道。也就输入\(X\)加上某个\(Z\)得到\(Y\)。

在这种情况下：\[q(y|x) = P_Z(y-x) = P_Z(z).\]

我们希望求得的是： \[ C(P_S) = \max_{p(x):\mathbb{E}_X[X^2] \leq P_S} I(X;Y) = \max_{p(x):\mathbb{E}_X[X^2] \leq P_S} [h(Y) - h(Z)]. \] （这里的\(\mathbb{E}_X[X^2]\)实际上是物理意义上均值为0的X的功率，因此这个约束是功率的约束） 之所以能得到上面的结论，因为： \[ \begin{aligned} h(Y|X) &= -\iint_{XY}P_X(x)q(y|x) \log q(y|x) dxdy\\ &=-\iint_{XZ}P_X(x)P_Z(z) \log P_Z(z) dxdz\\ &= -\int_z P(z) \log P(z)dz \\ &= h(Z) \end{aligned} \] 因此在这个情况下：\(h(Y|X) = h(Z)\)

高斯噪声

现在我们假设这个噪声为高斯噪声。

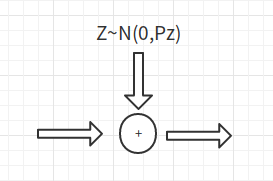
则： \[ \mathbb{E}[Y^2] = \mathbb{E}[(X+Z)^2] = \mathbb{E}[X^2]+\mathbb{E}[Z^2] = P_S+P_Z \] 如果回顾连续随机变量的熵和互信息，我们可以得到： \[ \max_{p(x):\mathbb{E}[x^2]\leq P_S}h(Y) = \frac 1 2 \log 2\pi e(P_S+P_Z) \] 而\(h(Z) = \frac 1 2 \log 2 \pi e P_Z\) 而这时候，我们可以得到： \[ \begin{aligned} C(P_S) &= \max(h(Y) - h(Z)) = \frac 1 2 \log \frac{P_S+P_Z}{P_Z} \\ &=\frac 1 2 \log(1+\frac{P_S}{P_Z}) \end{aligned} \]

上式中，\(\frac{P_S}{P_Z}\)也就是常说的信噪比。可以看到，如果想要增加容量，我们可以想方设法提高信源功率，或者减少噪声。这是一个非常重要的公式，拓展到模拟信道的情况上，我们就可以得到著名的香农公式。

实际上，对于高斯分布的输入，高斯噪声具有最大的破坏力。即，在同样的功率约束条件下，加性高斯噪声使得信道的容量最小。

对于无记忆加性噪声信道，若输入信号\(X\)具有高斯分布，加性噪声的功率为\(P_N\)，则当噪声具有高斯分布的时候，输入输出的互信息达到最小。

这一点并不难理解，因为噪声带来的影响在最终是要被去除的，而高斯情况下熵最大，去除的越多，留下的越少，所以使得信道容量最小。

一般的无记忆加性噪声信道容量

现在我们来看看一般的无记忆加性噪声的信道容量。

首先，我们必须明确，如果噪声是任意分布的，我们无法获得信道容量的解析解，但是我们可以给出其上界和下界。

  • 下界： \[ \begin{aligned} C(P_S) &= \max_{P(X)} \{I(X;Y):\mathbb{E}[X^2] = P_S\}\\ \ge I(X_G;Y)\ge I(X_G;Y_G) = \frac 1 2 \log(1 + \frac{P_S}{P_Z}) \end{aligned} \]

因为上面我们已经得到了。高斯噪声的破坏力是最大的。

  • 上界： \[ \mathbb{E}[Z^2] = P_N,\mathbb{E}[X^2] = P_S,\mathbb{E}[Y^2] = P_S+P_N\\ h(Y)\leq \frac{1}{2}\log [2\pi e (P_s +P_N)]\\ C_(P_S) \leq h(Y) - h(Z) = \frac 1 2 \log[2\pi e \frac{P_S+P_N}{P_e}]\\ \] 上式中： \[ P_e \triangleq \frac 1 {2\pi e} \exp[2h(Z)] \]

说实话，我并不知道这个定义是从何而来。而且\(P_e\)中还包含着\(h(Z)\)，又怎么能说是个上界呢？

并联连续高斯信道

输入\(X_n,P_{S_n}\)，信道噪声\(Z_n,P_{N_n}\).

在总功率限定的情况下，求信道容量-费用函数： \[ C(P_S) = \sup_{P(X)}\{I(X;Y):\sum_{n=1}^N P_{S_n} = P_S\} \] （这里的sup指的是Supremum，上确界）。

现在我们面临一个优化问题： \[ \max I(X^n;Y^n) = \sum_i \frac{1}{2} \log (1+\frac{P_{S_i} }{P_{N_i} }) \] s.t. \(\sum_{i=1}^n P_{S_i} = P_S,P_{S_i} \ge 0\)

这个优化问题解决如下： \[ \frac{\partial }{\partial P_{S_i} } \left[\sum_{i=1}^n \frac{1}{2} \log(1+\frac{P_{S_i} }{P_{N_i} }) - \lambda (\sum_{i=1}^n P_{S_i} - P_S)\right] = 0\\ \frac{1}{2} \frac{P_{N_i} }{P_{S_i}+P_{N_i} } \frac{1}{P_{N_i} } - \lambda = 0, \text{for }1 \leq i \leq n\\ P_{S_i} + P_{N_i} = \frac{1}{2\lambda_i}, \lambda = \frac{n}{2(P_S+P_N)}\\ P_{S_i} = \frac{P_S+P_N}{n} - P_{N_i}, \]

要注意，这里我们将信道个数总数写成了\(n\)，而\(P_N\)表示的是噪声功率。

有时候，我们发现，求得的\(P_{S_i}\)，也就是给该信道分配的功率是小于0的，这时候应该怎么办？ #### 注水功率 #### 下面介绍一个很形象的概念，叫注水功率。如下图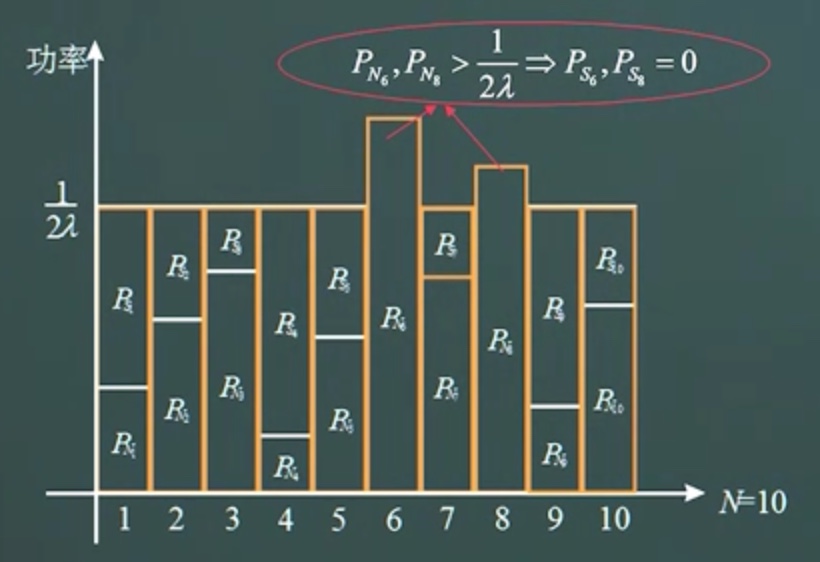： 可以看到的是，有的时候水是无法覆盖住某些地方的。这说明的是这个信道的噪声太大了，所以我们应该将其弃用。然后再重新计算这个功率的分配，直到没有负值。

模拟信道容量

模拟信道在时间和取值上都是连续的信道。是自然界最自然的一种信道，如电磁波，光纤，电缆等传播。

然而实际中模拟信道在数学上的研究是难以进行的。我们只研究最简单的一类模拟信道：AWGN信道。 ### AWGN信道 ### AWGN（Additive White Gaussian Noise）信道有下面几个特点： * 带宽有限：\(W\) * 加性噪声：\(y(t) = x(t) + z(t)\) * 白色噪声：平稳遍历随机过程，功率谱密度均匀分布于整个频域，即功率谱密度（单位带宽噪声功率）为一常数 * 高斯噪声：平稳遍历随机过程，瞬时值的概率密度函数服从高斯分布

这个信道描述如下：

输入信号：\(x(t)\) * 带宽有限：输入信号带宽限制在\([-W,W]内\) * 时间有限：T

输出信号：\(y(t)\)

噪声信号：\(z(t)\) * 加性白色高斯噪声 * 零均值 * 双边功率谱密度：$N(f) = \left { \[\begin{matrix} \frac{N_0}{2} & \vert f\vert \leq W\\ 0&\vert \vert > w \end{matrix}\]

. $

信道费用：输入信号的功率

信号的正交分解

  • 由于信道频带受限，信号时长受限，所以仅需要\(N = 2WT\)个采样点就可以表示
  • 因此信道在时间上可以被离散化为\(2WT\)个点，在每个点上取值连续
  • 这样变成了并联的连续信道 实际上，上面的采样就是著名的奈奎斯特采样。

之前我们说明了并联的连续信道的容量求法，但是前提是各个信道是独立的。现在我们必须要明白，经过采样的这\(N = 2WT\)个信道是否互相独立？

答案是独立的。为了验证他们的独立性，我们只需要验证它们不相关即可，因为在高斯分布下，不相关就意味着独立。证明如下： (额，这里也不是很懂。对于信号处理和通信方面的知识已经忘的差不多了)

对于\(N\)个信道，两两独立，每个噪声功率为\(\frac{N_0}{2}\).

所以利用时域上采样定理将信号变成离散序列后，模拟信道可看成加性白色高斯噪声无记忆连续信道，相当于\(N\)个高斯加性信道的并联信道。这时候我们可以用注水功率来分配这个功率。

并联信道总容量费用函数\(C_T(P_S) = \frac{1}{2} \sum_{n=1}^{2WT} \log (1+ \frac{P_{S_n} }{P_{N_n} })\)

噪声约束：\(P_{N_n} = \frac{N_0}{2} \rightarrow P_N = NP_{N_n} = 2WT\frac{N_0}{2} = WTN_0\)

功率约束：（类似于注水功率分配） \[ P_{S_n} = \frac{P_ST+P_N}{N} - P_{N_n} = \frac{P_ST+2WT\frac{N_0}{2} }{2WT}-\frac{N_0}{2} = \frac{P_S}{2W} \]

这时候，我们就得到了香农公式，AWGN信道的容量为： \[ C = W \log (1+\frac{P_S}{N_0W}) \] 上式中，各个量的单位为\(C-bps,W-Hz\)或者\(s^{-1}\),\(P_S-Watt,N_0-Watt/Hz\)

Vision:提升容量的各种手段

  • 增加带宽 \[ \lim_{W\rightarrow \infty}C(P_S) = \lim_{W\rightarrow \infty} \frac{P_S}{N_0}\log\left(1+\frac{P_S}{N_0W}\right)^{\frac{N_0W}{P_S} } = \frac{P_S}{N_0} \log e \approx 1.44\frac{P_S}{N_0} \]

  • 增加带宽 \[ \lim_{P_S \rightarrow \infty} C(P_S) \approx \ln\left(\frac{P_S}{N_0W} \right) \]

因此，对于同样容量的传输要求，可以采用两种方式：减少带宽，发送较大功率的信号，或者增加带宽，用较小功率的信号传输。

可以看到的是，我们可以不断增加带宽来增加信道容量，不过这个性价比会越来越低，因为这是一个log函数。

Vision:信息与热力学的联系

这里有一个有意思的信息论角度对阿波罗登月的证伪，大家图一个乐，里面有很多假设和实际不符。 到目前为止，我们都只算出来了信道容量，没有讲过怎么编码能得到这些容量。接下来要做的就是说明，所有上面算出来的容量，都是可以实现的。 ## 信道编码 ##

这里我们先回忆一下之前的混乱打字机。之前说过，世界上任何一个数字信道，都可以直接或者间接地看作是混乱打字机模型。

对于信道\(\{X,q(y|x),Y\}\)的信道编码包含以下要素： * 输入符号集合\(\{1,2,...,2^{nR} \}\) * 编码函数\(X^n\):\(\{1,2,...,2^{nR} \}\rightarrow X^n\)，该函数为每一个输入符号产生了相应的信道编码码字\(X^n(1),X^n(2),...,X^n(m)\)，这些码字构成的集合称为“码本”。 * 解码函数\(g\):\(Y^n \rightarrow \{1,2,...,2^{nR} \}\)，该函数为一个确定性判决函数，将每一个可能的接受向量映射到一个输入符号。

意思也就是，对于符号个数为\(2^{nR}\)的符号集，我们把它映射到一个长度为n的序列上,分n次传输。 ### 信道编码的码率 ###

\((M,n)\)码的码率Ｒ定义为： \[ R = \frac{\log M}{n} , \] 单位为比特/传输。这是信道码的每个码字母所能携带的最大的信息量。

如何理解？对于输入集合如果取等概分布，则它的信息量为\(M\)，这时候呢，\(n\)次传输才能传达这么多的信息量，所以每个传输的量就是\(\frac{\log M}{n} = R\)，则\(M = 2^{nR}\)。称这样的码为\((2^{nR},n)\)码。

Example

重复码，输入字母数\(M = 2\):\(\{0,1\}\)，重复n次，这个码率为\(1/n\)。

二进制奇偶校验码，输入字母数\(M = 2^{n-1}:{x_1,x_2,...,x_{n-1} }\)，信道编码方案为\(C = x_1,x_2,...,x_{n-1}x_{\text{parity} }\)，其中\(x_{\textP{parity} }\)用于辨识码字中\(1\)的个数为奇数还是偶数，这个码率为：\(\frac{n-1}{n}\)。

信道编码的错误概率

输入为符号\(i\)时的条件错误概率为： \[ \begin{aligned} \lambda_i &= Pr\{g(Y^n) \ne i \vert X^n = x^n(i)\}\\ &= \sum_{y^n} q(y^n\vert x^n(i))I(g(y^n) \ne i) \end{aligned} \] 其中\(I(\cdot)\)为指示函数。

\((M,n)\)码的最大错误概率为： \[ \lambda^{(n)} = \max_{i \in 1,2,...M} \lambda_i \]

\((M,n)\)码的算术平均错误概率为： \[ P_e^{(n)} = \frac{1}{M} \sum_{i=1}^M\lambda_i \]

我们称一个码率\(R\)是可达的，若存在一个信道编码\((\lceil 2^{nR}\rceil,n )\)，其最大差错概率在\(n\rightarrow \infty\)时趋于0。可以看出来可达要求无差错，而且是渐进的。

这时候我们得到信道容量的另外一个定义：一个信道的容量是该信道上所有可达码率的上确界，即\(C = \text{sup }R\)，这意味着\(C\)一定对应着一种信道编码方案。

经验主义式的设计

在信道传输中如何减少差错？由香农公式： \[ C_T(\beta) = WT \log(1+\frac{P_S}{N_0W}) \] 可以得到，提高抗干扰能力的方法如下： 1. 增加功率(提高信噪比) 2. 加大带宽(信号变化剧烈) 3. 延长时间(降低速率)

\(C = max_{p(x),功率约束}\{I(X;Y)\}\)

而降低重复速率，实际上就是重复，增加冗余。

重复码

最直观的纠错方法就是：重复，增加冗余。 * 编码１：将每个输入元重复三次 * 纠正任一位上的错误 * 设码字记为\((c_8,c_7,...,c_0)\) * 由编码方法可知，信道无误时： \[ c_8 = c_7 = c_6\\ c_5 = c_4 = c_3\\ c_2 = c_1 = c_0 \] * 解码时，若\(c_8 = c_6 \ne c_7\)，则判定\(c_7\)位出错，采用简单多数法进行判定 * 依据是：连续出现两个错误的概率远远小于出现一个错误的概率 如下图，如果我们将上述编码放进二进制对称信道，则想要得到无差错编码，\(n \rightarrow 0\)，而码率也趋近于0，这不是一个好消息。

但是，是否对于信息的无差错传输，就意味着码率为0呢？答案是否定的。

现在我们考虑BSC信道，\(W= \{1,2,...,2^k\}\),如图：

我们可以得到： \[ \begin{aligned} nC \ge nI(X;Y)\\ \ge I(X^n;Y^n)\\ \ge I(W,\hat W)\\ =H(W) - H(W\vert \hat W)\\ \ge k - k H(P_e) \end{aligned} \] 上式中最后一步是有Fano不等式得到的。

则：\[k \leq \frac{nC}{1 - H(P_e)}\]

而由于BSC信道的容量可以得到：\(C = 1 - H(P)\)，所以我们得到一个R的上界： \[ R = \frac{k}{n} \ge \frac{1 - H(P)}{1 - H(P_e)} \]

通过变形，我们可以得到： \[ H(P_e) \ge 1 - \frac C R \rightarrow P_e \ge H^{-1}\left(1 - \frac C R\right) \]

这意味着，如果想要让\(P_e\leq 0\)，则\(R \leq C\)，如果\(R > C\)，则\(H(P_e)>0\)，所以我们一定可以得到\(P_e>0\)，不可能进行可靠通信。

那么无差错传输的情况下，码率最大能有多少？先给你看一个preview，很直白的内容，不过它被证明确实是正确的：

想象信道将信源映射到一个球体里，而对每个输入符号也对应一个球。而这个球的体积就意味着噪声带来的体积，而大球中能容纳多少小球，正是这个信道编码在无错的情况下可以映射的符号数M。因为这个球的维度是n维的，我么可以得到： \[ M = \frac{\left[\sqrt{P_S +P_N}\right]^n}{\left[\sqrt{P_N}\right]^n} = (1 + \frac{P_S}{P_N})^{\frac n 2} \]

由上式，可以计算得出： \[ R = \frac 1 2 \log (1 + \frac{P_S}{P_N}) \]

而这个值，正好与连续无记忆加性高斯噪声信道的容量一致。

当然，这个只是preview，不是严格的证明过程。下面对这个证明进行稍微严谨地推导，说明大多数噪声信道都有这样地特性。

为了证明这个东西，我们需要介绍一些别的定义。之前证明信源无失真压缩定理地时候，用到了典型序列，而这次我们在典型序列地基础上，重新介绍一个新的内容。 ### 证明香农第二定理 ### #### 联合典型序列 #### 设\((X^n,Y^n)\)是长为\(n\)的随机序列对，其概率分布满足 \[ p(x^n,y^n) = \prod_{i=1}^n p(x_i,y_i) \] 若\((X^n,Y^n)\)满足以下条件，则称其为联合典型序列： * \(\lvert -\frac 1 n \log p(x^n) - H(X) \rvert < \epsilon\) * \(\lvert -\frac 1 n \log p(y^n) - H(Y) \rvert < \epsilon\) * \(\lvert -\frac 1 n \log p(x^n,y^n) - H(X,Y)\rvert < \epsilon\) 联合典型序列构成的集合为\(A_\epsilon^{(n)}\)。

联合典型序列与之前典型序列定义是有很大地相似性：信息论——Lossless-Encoding.我们首先要看看联合典型序列的性质，才能用它来证明。 #### 联合渐进等同分割定理（Joint AEP） #### 设\((X^n,Y^n)\)是长度为\(n\)的随机序列对，其分布满足： \[ p(x^n,y^n) = \prod_{i=1}^n p(x_i,y_i) \] 则以下性质成立： * 当\(n \rightarrow \infty\)时，\(Pr((X^n,Y^n) \in A_\epsilon ^{(n)}) \rightarrow 1\) * \((1 - \epsilon)2^{n(H(X,Y) - \epsilon)} \leq \vert A_\epsilon ^{(n)} \vert\leq 2^{n(H(X,Y)+\epsilon)}\) * 设$(,)p(xn)p(yn) \(,即\),\(统计独立，且具有与\)p(xn,yn)$一致的边缘分布，则： \[ Pr\left((\tilde{X^n},\tilde{Y^n}) \in A_\epsilon ^{(n)}\right) \leq 2^{-n(I(X,Y) - 3\epsilon)} \] 若\(n\)足够大，则： \[ Pr\left((\tilde{X^n},\tilde{Y^n}) \in A_\epsilon ^{(n)}\right) \ge (1 - \epsilon)2^{-n(I(X,Y) + 3\epsilon)} \]

前两点都比较好理解，第三点中，\((\tilde{X^n},\tilde{Y^n})\)是由\((X^n,Y^n)\)的边缘分布依照\(X^n,Y^n\)独立形成的另一个联合分布，而这个分布属于典型序列的概率约等于\(2^{-nI(X,Y)}\)。

在这里我们证明以下第三条的前半部分： \[ \tilde{X^n},\tilde{Y^n}\text{ are independent. }\tilde{X^n}\sim P_X(x^n),\tilde{Y^n}\sim P_Y(y^n)\\ \begin{aligned} Pr\{(\tilde{X^n},\tilde{Y^n}) \in A_\epsilon^{(n)} \} &= \sum_{(\tilde{x^n},\tilde{y^n}) \in A_\epsilon^{(n)} } P(x^n)P(y^n)\\ &\leq 2^{b(H(X,Y) + \epsilon)}\cdot 2^{-n(H(X) - \epsilon)} \cdot 2^{-n(H(Y) - \epsilon)}\\ &= 2^{-n(I(X,Y) - 3\epsilon)} \end{aligned} \]

下图可以帮助我们更好地理解这些性质： * 联合分布中，大约有\(2^{nH(X)}\)个典型X序列和\(2^{nH(Y)}\)个典型Y序列 * 其组合共有\(2^{nH(X) + nH(Y)}\)个，但是其中联合典型的只有\(2^{nH(X,Y)}\)个 * 随机选择而出现联合典型序列的概率为\(2^{-nI(X,Y)}\)

现在来看一下联合典型序列的另一个解释： * 对于典型输入序列\(x^n\)，存在大约\(2^{nH(Y|X)}\)个可能的输出，且它们等概 * 所有可能的典型输出序列大约有\(2^{nH(Y)}\)个，这些序列被分成若干个不相交的子集 * 子集个数为\(2^{n(H(Y) - H(Y|X))} = 2^{nI(X;Y)}\)，表示信道可以无错误传递的最大字母序列个数

可达性的证明

可达性的证明也就是我们可以找到一个编码函数和解码函数，使得信道带到容量C，而且是无差错地传输。 \[ W \in [1:2^{nR}] \rightarrow X^n \sim P_X(x) \rightarrow q(y|X)\rightarrow Y^n \hat W \]