Learning From Data——PCA

Posted on 2018-11-19 Edited on 2018-12-07 In 数据学习课程

上节课除了介绍了K-Means，更重点介绍了另外一个算法，PCA（Principal Component Analysis）。

PCA中文应该翻译为主要成分分析。这个翻译是直白的，我们也能很容易知道猜得到这个算法在做什么。

首先举个例子：

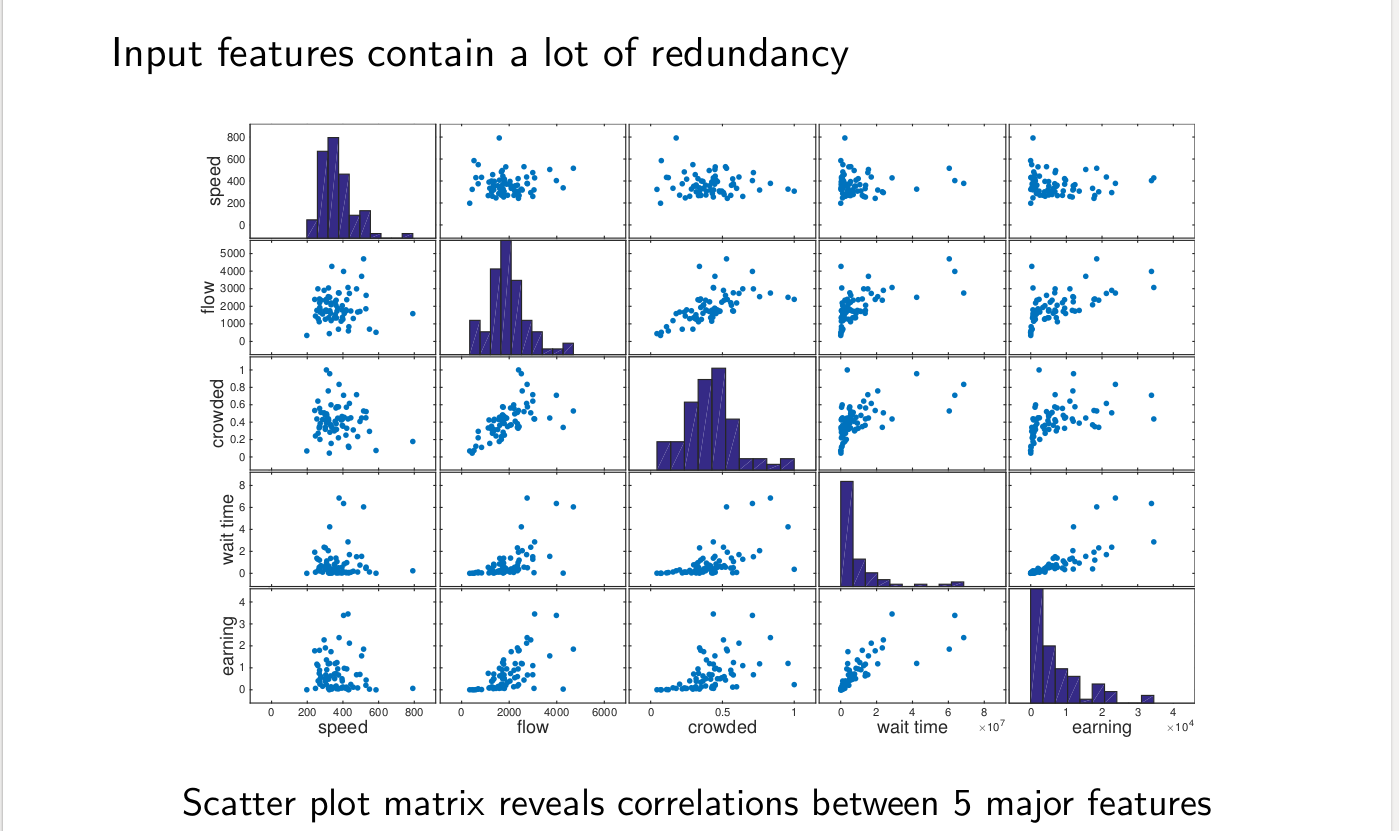
从上面看出来，有时候很多特征包含了很多的冗余信息。如拥挤程度和人流密度，就有很大的相关性。

我们需要消除这样的相关性，并且减少噪声。 ## PCA描述 ## PCA算法的描述如下：

给定输入${X_1,X_2,...,X_m}，X_i \in \mathbb{R}$.找到输入的一个线性，正交转换W：$\mathbb{R}^n, \mathbb{R}^k$。W将最大方差方向与新空间的坐标轴对其。

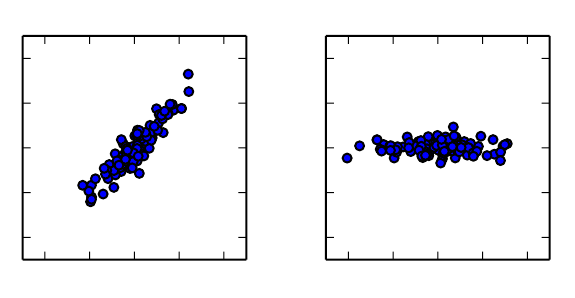
如下图：左侧图片中，$x_1$与$x_2$是高度相关的，右侧图为转换过后的z，它几乎和水平坐标轴平行。

推导PCA

为了方便PCA的推导，我们首先会对数据进行预处理，也就是对其进行normalize,使得Mean(X) =0,Stdev(X) = 1: \[ X_i := X_i - Mean(X) \leftarrow recenter\\ X_i := X_i / Stdev(X) \leftarrow scale \]

Stdev(X)为标准偏差函数。

我们希望在输入中找到让各个样本变化最大的方向的主轴u（找到变分单位向量的主轴），如下图：

PCA的目标： 1. 找到互相正交的主要成分$u_1,u_2,...,u_n$，它们之间互不相关。 2. 大多数X中的变化会被k个主要成分代表了，这里的$k << n$.

根据PCA的目标，我们可以分析PCA的主要步骤： 1. 找到X在某个向量上的投影，使得$u_1^TX$有最大的方差。 2. 对于j=2,...n，继续上面的步骤，找到X在某个向量上的投影（与之前的向量正交），使得$u_j^TX$有最大的方差，再次强调：$u_j$与$u_1,...,u_{j-1}$正交。

因为$\Vert u \Vert = 1$,则$X_i$在$u$上的投影长度为：$X_i^Tu$.而这些投影的方差计算结果如下： \[ \begin{aligned} \frac 1 m \sum_{i=1}^m (X_i^T u)^2 &= \frac 1 m \sum_{i=1}^m u^TX_iX_i^T u \\ &= u^T (\sum_{i=1}^m X_i X_i^T)u\\ &= u^T \Sigma u \end{aligned} \] 这里的$\Sigma$是$X$的协方差矩阵。

找到单位向量$u_1$使得投影的方差最大，可以用数学语言描述如下： \[ u_1 = argmax_{u:\Vert u \Vert = 1} u^T\Sigma u \]

$u_i$是X的第i个主要成分。

如何求解$u_i$呢？首先，既然$u_i$要与之前的正交，因此这个求解顺序是从1到n。现在我们来分析$u_1$。

命题1

$u_1$是协方差矩阵最大的特征向量(eigen vector)。

证明如下：

首先，根据数学描述构建Lagrange function： \[ L(u) = -u^T \Sigma u + \beta (u^Tu - 1) \]

to minimize $L(u)$:

\[ \frac{\partial L(u)} {\partial u} = -\Sigma u + \beta u = 0 \]

因此我们可以确定了u是一个$\Sigma$的特征向量。

同时,投影方差等于$u^T u = u^T u = $.

为了让方差最大，也就是$\beta$最大。而最大的特征值对应这最大的特征向量。

命题2

第j个X的主要成分，也就是$u_j$为$\Sigma$的第j个最大的特征向量。

为了简化问题，先写出第二个主要成分的数学描述： \[ u = argmax_{u:\Vert u\Vert = 1;u_1^T u = 0} u^T \Sigma u \]

同样地构建Lagrange Function： \[ L(u) = -u^T\Sigma u + \beta_1 (u^Tu-1 ) + \beta_2 (u_1^Tu) \]

\[ \frac{\partial L(u)} {\partial u} = -\Sigma u + \beta_1 u + \beta_2 u_1 = 0 \]

上式中，我们知道两个互相正交的非零向量加起来不可能为0.所以得到：

$_2 = 0, u = _1 u $

所以按照证明命题1同样的步骤，我们就证明了命题2中的第二个主要成分是成立的.

同样的证明方法可以继续拓展，$j=3,...,n$，都是成立的。

PCA的性质

从上面的推导，我们可以得到的PCA的下面几个性质：

主要成分投影的方差分别为：

$Var(X^Tu_j) = u_j^T \Sigma u_j = \lambda_j,j=1,2,...,n$

不同方差的百分比$\frac {\lambda_j}{\sum_{i=1} ^n \lambda _i}$也就是主要成分的所占比重，也说明了各个主要成分之间是不相关的。

PCA投影

确定主要成分后，我们通过将原数据对主要成分投影来得到数据的压缩等效果。也就是：

$Z_i = [X_{i}^T u_1,X_i^T u_2,...,X_i^T u_n]$

使用矩阵形式： \[ \begin{aligned} Z &= \begin{bmatrix} x_{1}^T& X_{2}^T& ...& X_{m}^T \end{bmatrix}\begin{bmatrix} |&|&...&|\\ u_1 & u_2& ... & u_n\\ |&|&...&| \end{bmatrix} &=XU \end{aligned} \]

或者$Z_i = U^TX_i$。

我们可以看出来，$Z_i$同样是n维度的。而截断转换$Z_k = XU_k$只保留前k个主要成分，用来做维度的压缩，因为前k个主要成分往往占了内容的大部分。

PCA在做什么？

PCA删除了输入X中的冗余数据：

如果经过转换后为Z，则 $cov(Z) = \frac 1 n Z^T Z = \frac 1 n (XW)^T (XW) = \frac 1 n W^T(X^TX)W = \frac 1 n W^T\Sigma W$.

由于$\Sigma$是对称矩阵，因此它有实特征值。它的特征分解(eigen decomposition)为： \[ \Sigma = W Λ W^T，\\ where~W = \begin{bmatrix} |&|&...&|\\ u_1 & u_2& ... & u_n\\ |&|&...&| \end{bmatrix},Λ = \begin{bmatrix} \lambda _1 &0&\cdots&0\\ 0&\lambda_2&\cdots&0\\ \vdots & \vdots& \ddots &\vdots\\ 0&0&\cdots&\lambda_n \end{bmatrix} \]

因此： $cov(Z) = W^TW Λ W^TW = Λ $.主成分变换XW对角化了X的样本协方差矩阵.

PCA的著名例子：Iris Dataset，EigenFaces。

PCA的限制

PCA很有用，但是它也有一些明显的缺陷：

只考虑线性关系
假设数据是真实并且连续的
假设输入空间近似正态分布（不过在非正态分布中也可能工作得很好）下面是一个非正态分布的例子：

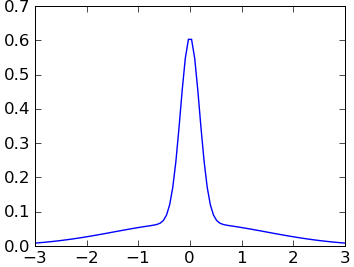
输入：

PCA投影：

下次我们将主要说明一下第一个缺陷的解决办法：kernel PCA。

k-means与PCA的对比

Unsupervised learning algorithm:

algorithm	low dimension	sparse	disentangle variations
k-means	no	yes	no
PCA	yes	no	yes