图形学——Viewing
上次图形学的博客中介绍了转换，所以我们可以从世界坐标转换到相机坐标了。不过虽然我们学的是三维模型，不过我们看到的都是二维的。近大远小是小学生都明白的道理，而一个物品的距离等等都会影响它在我们眼中,以及拍摄出来照片的样子。因此这次讲得内容是观察（Viewing）。 ## 正交投影（Orthographic Projection） ## 正交投影是最简单的一个投影方式。它实际上就是三维坐标中的点丢弃一个坐标轴，如我们需要将物体投影到xy平面上，我们就需要丢弃掉z轴。
它的特点：原来平行的线保持平行。这个特点使得它在很多工程制图中非常有用。
这个博客会介绍OpenGL中的正交投影（gluOrtho）实现。
在OpenGL中，gluOrtho做的实际上是将物体转换到一个中心位于坐标轴中心的正方体上。物体原来是个长方体，所以gluOrtho需要提供的是left,right;up,bottom;near,far.
为什么要这么做？这个是三维pipeline的一步，先映射到正方体上，最后方便投影到真正的屏幕上，也就是映射到平面像素上。
而映射到中心正方体的边长是2,左右（上下前后）坐标分别为-1,1. 因此如何映射？
假如提供的left，right;up，bottom;near,far分别值为l,r;u,b;n,f;既然要映射到正方体上，那么需要两部：一个平移，一个缩放。
首先是平移，平移向量很容易： \[ t = \begin{bmatrix} -\frac{l+r}{2}\\ -\frac{u+b}{2}\\ -\frac{n+f}{2} \end{bmatrix} \]
再一个是缩放。既然要缩放，比如左右距离的缩放，是从\(r - l\)缩放到2.因此缩放比例为：\(\frac{2}{r-l}\).
同样的道理，我们可以得到缩放矩阵： \[ S = \begin{bmatrix} \frac{2}{r - l}&0&0\\ 0&\frac{2}{u-b}&0\\ 0&0&\frac{2}{f - n} \end{bmatrix} \]
需要注意的是缩放的这些值都是正值。
然后通过齐次坐标将上面两个结合起来得到转换矩阵： \[ M = \begin{bmatrix} \frac{2}{r - l}&0&0&-\frac{r+l}{r-l}\\ 0&\frac{2}{u-b}&0&-\frac{u+b}{u-b}\\ 0&0&\frac{2}{f - n}&-\frac{f+n}{f-n}\\ 0&0&0&1 \end{bmatrix} \]
不过事情还没完。要知道，在OpenGL中，规定我们观察的方向是Z轴的负向（也就是在视点坐标中，x,y的坐标都是有正有负的，但是我们往前看到的东西的z坐标都一定是负的）。所以上面的式子就要有点变化了，我们仍然希望远的投影到+1,而近的投影到-1,这就要求实际上不光要平移到原点，在缩放时候还要将远近两个面颠倒。这时候平移大小变为：\(\frac{f+n}{2}\)(因为实际坐标是-f,-n),而为了让远的投影到1,而近的投影到-1,这个缩放尺度就要变成负数，使得位置颠倒，因此缩放尺度变为：\(-\frac{2}{f-n}\)，最后乘进去后，变化的只有一小部分： \[ M = \begin{bmatrix} \frac{2}{r - l}&0&0&-\frac{r+l}{r-l}\\ 0&\frac{2}{u-b}&0&-\frac{u+b}{u-b}\\ 0&0&-\frac{2}{f - n}&-\frac{f+n}{f-n}\\ 0&0&0&1 \end{bmatrix} \]
也就是，实际上，只有一项变化了。需要注意的是这里的f和n都是正值。
透射投影（Perspective Projection）
透射投影中，远处的景色总是更近一点。实际上这就是透射投影。
下面说的这个东西和SLAM中说的针孔模型很相似：假如有一个点坐标为\(X,Y,Z\)，而面前有一个屏幕，到针孔的距离为d（d>0），那么在屏幕上这一点的投影为： \[ X' = -d\frac X Z\\ Y' = -d\frac Y Z \]
这里负号的存在，还是因为z坐标都是负的。
而我实际上我们可以将透射投影转换写成这样： \[ P = \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ 0&0&-\frac {1}{d}&0 \end{bmatrix} \]
这个矩阵乘起来之后之前的坐标都没有改变，除了最后一项1变成了\(-\frac Z d\). 而齐次坐标如果将最后一个转化为1,则之前的X，Y，Z变成了：\(-d\frac X Z, -d\frac Y Z,-d\).这是个很巧妙的转换。
而OpenGL中的透投影函数会更复杂一点。我们还是通过说明gluPerspective，来理解透射映射。
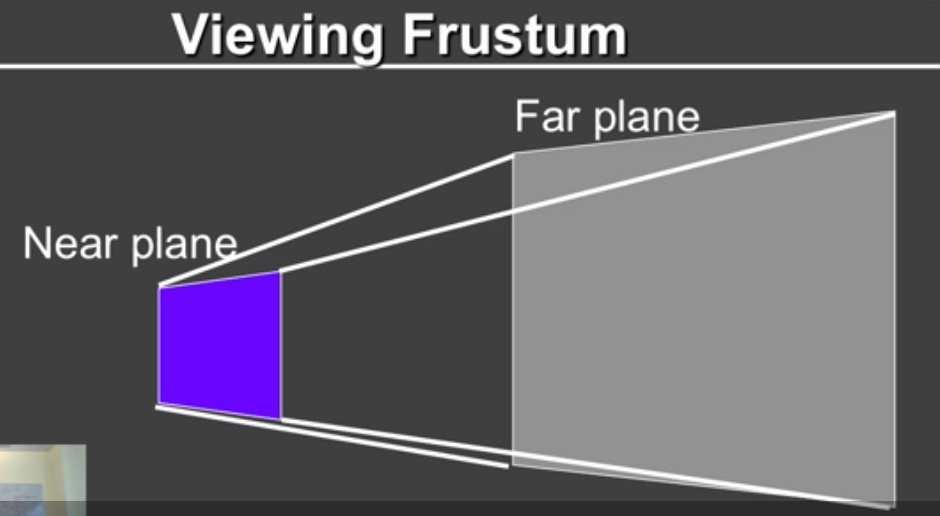
首先我们需要定义一个新的名词，叫做Viewing
Frustum(视锥体)。一个视锥体如下图： 
任何近裁面近的点或者比远裁面远的点都会被遮挡。
gluPerspective的参数需要：fovy，aspect,zNear,zFar(zNear,zFar>0,后文简写为\(Z_n,Z_f\)). fovy为视野，可以理解为眼睛睁得大小程度，而aspect定义了视锥的高宽比。
gluPerspective依然是将这个视锥体的投影结果转换到坐标轴的中心正方体（边长为2），使得近截面的z坐标为1,远截面的z坐标为-1.
而zNear和zFar代表了我们需要透射投影的最近距离和最远距离。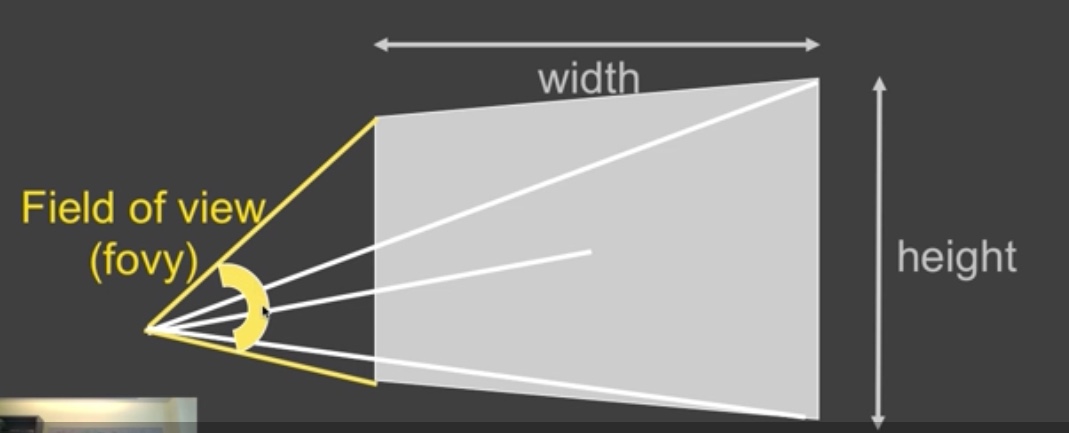 
投影到的"屏幕"由下图确定，（其中投影屏幕高为两个单位）： 
因为要映射到最后的中心正方体（变长为2），所以这个“屏幕”的高已经已经确定了，所以d的距离由\(\theta\)确定，而\(\theta = \frac {fovy}2，d = \cot
\theta\).另一方面，高确定为2,
因此aspect实际上改变最终投影的宽窄，由之前的基础，我们先这样写下这个式子：
\[
P = \begin{bmatrix}
\frac 1 {aspect}&0&0&0\\
0&1&0&0\\
0&0&1&0\\
0&0&-\frac {1}{d}&0
\end{bmatrix}
\]
既然齐次坐标最终最后一项要转化为1，也就是同时乘以某个数不会影响齐次坐标的大小，我们可以将上面个的矩阵写成： \[ P = \begin{bmatrix} \frac d {aspect}&0&0&0\\ 0&1&0&0\\ 0&0&A&B\\ 0&0&-1&0 \end{bmatrix} \]
因为我们最后要影响Z坐标，所以需要改变的值是A和B的位置，而不能让他们为0.从上式求得坐标： \[ p' = \begin{bmatrix} \frac d {aspect}&0&0&0\\ 0&d&0&0\\ 0&0&A&B\\ 0&0&-1&0 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix} = \begin{bmatrix} \frac {dx}{aspect} \\ dy\\ Az+B\\ -z \end{bmatrix} = \begin{bmatrix} -\frac {xd}{aspect*z} \\ -\frac{yd}{z}\\ -A-\frac B z\\ 1 \end{bmatrix} \]
因为我们要让远裁剪面在-1，近裁剪面在+1，因此： \[ \left \{ \begin{matrix} -A-\frac B {-Z_f} = 1\\ -A - \frac B {-Z_n} = =-1 \end{matrix} \right . \]
得到： \[ A =-\frac{Z_f+Z_n}{Z_f-Z_n} \\ B = -\frac{2 Z_n Z_f}{Z_f - Z_n} \]
因此将A，B带入后就是最后gluPerspective得到的矩阵。
Note
- 在这里我们不能将\(Znear\)设置为0,如果那样的话，会导致深度信息无法解析。
- fovy视野越大，我们看到的对象变得越小，这是因为屏幕大小是固定的。
- 我不明白为什么openGL要将这个映射到立方体上做的这么复杂，更远的地方（z值更小）映射到1。不过gluPerspective只是一部分，除了透射投影以外，还要得到得到平面坐标，然后映射到屏幕上。
- 传入函数的near，far，计算的到的d等都是距离，也就是都是正值，但是为了处理负的坐标值，多了很多麻烦。