数字图像处理——图像压缩

形态学是生物的一个分支，用来研究动植物的形状和结构。而这里的形态学图像处理，指的是提取图片中关于形状结构的组成承认，比如边界，骨架以及凸包（convex hull）。

集合论的概念

关于形态学图像处理离不开集合的一些操作，因此在这里先说明写一下可能会用到的操作。

属于\(\in\)，不属于\(notin\),子集\(\subset\)，并集\(\cup\)，交集\(\cap\)，空集\(\emptyset\)，补集\(A^c\)，两个集合的差：\(A - B = A \cap B^c\)。

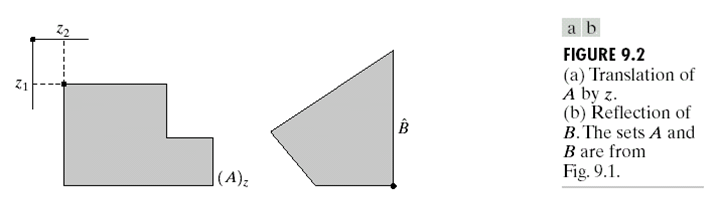
集合的反射：\(\hat B = \{w \vert w = -b, b \in B\}\)；

集合的平移：\((A)_z = \{c\vert c = a + z , \text{for }a \in A\}\)

二进制上的布尔操作规则如下：

形态学图像处理

转换不变（shift-invariance）

在二值图上的逻辑操作是形态学图像处理。转换不变定义如下：

我们可以看出来，转换不变也就是这个转换不会改变位置。需要注意的是，转换不变并不意味着是线性的。

SE（Structure Element）

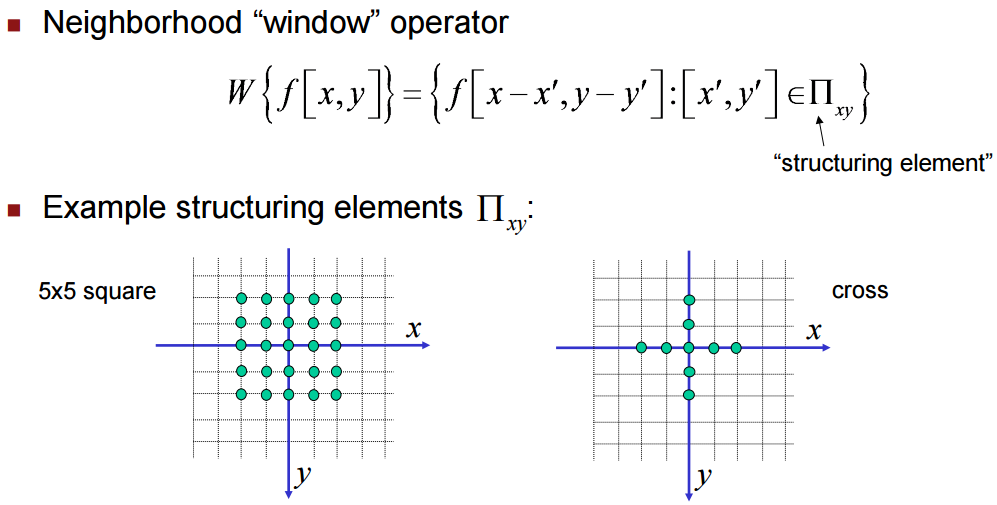
结构元素用来探测一个图片，可以把他当成滤波器的窗口，mask等等，类似的东西。不过它的形状是可以任意的：

腐蚀（Erosion）

\(A,B\)是二维空间中的几何，而将A用B腐蚀定义为： \[ A \ominus B = \{z \vert (B)_z \subset A\} \] 这里的z是一个平移量，也就是如果\(B\)经过平移\(z\)之后还被\(A\)完全包含，那么所有这些平移量(z是平移量，这里指的应该是\(A\)在\(z\)处的值)就被定义为\(A\)被\(B\)腐蚀。这个操作可以让\(A\)变小一圈：

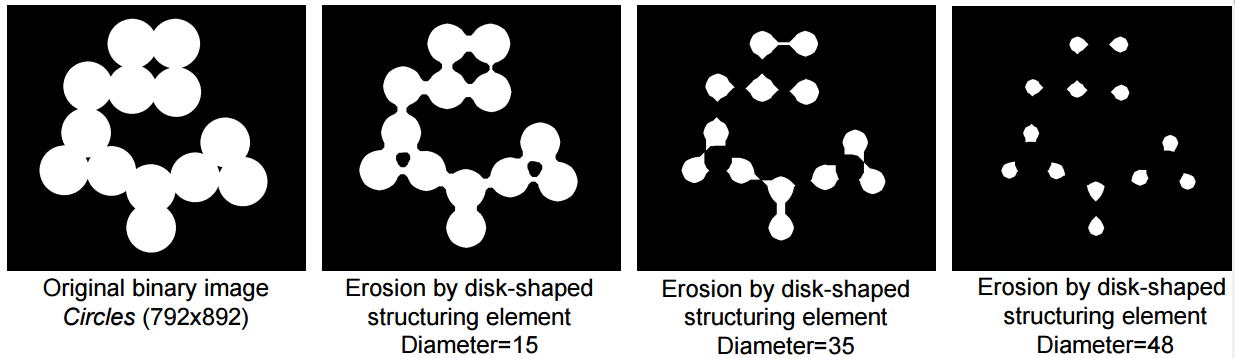
在二值图片上，它的表现就是，用一个SE要游动，SE中的值都是1，而如果SE与某一块的\(A\)取交集，全部得到1，那么该中心的值取1，否则取0。这个操作如下图：

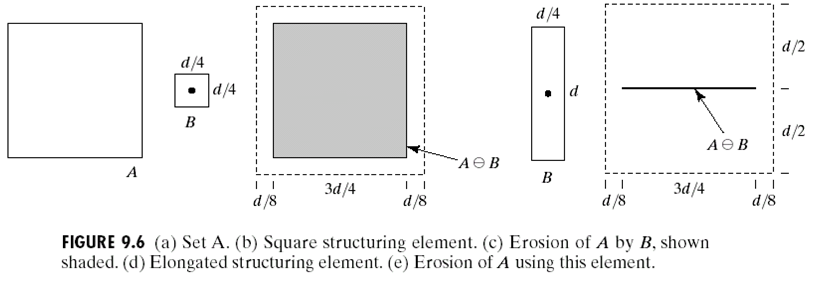
上面这张图中，白色表示1，而黑色表示的是0。侵蚀会侵蚀掉所有的小方块，而对于比自己大的方块，它不会完全消失，而是会保留靠近中心位置的白色。因此通过侵蚀我们可以来去除图片中一些不想要的像素。不过侵蚀后得到小的方块又如何复原？这需要用到下一个操作：膨胀。

膨胀（dilation）

将A用B膨胀的定义如下： \[ A \oplus B = \{ z \vert (\hat B)_z \ne \emptyset\} \] 我们知道\(\hat B\)是反射，因此所有在\(\hat B\)上的平移，只要A与平移后的\(\hat B\)有重叠区域（腐蚀需要全部重叠，也就是A包含平移后的B），那么该平移就属于膨胀。

膨胀的效果如下：

膨胀操作是腐蚀操作的对偶操作： \[ (A \ominus B)^c = A^c \oplus \hat B \]

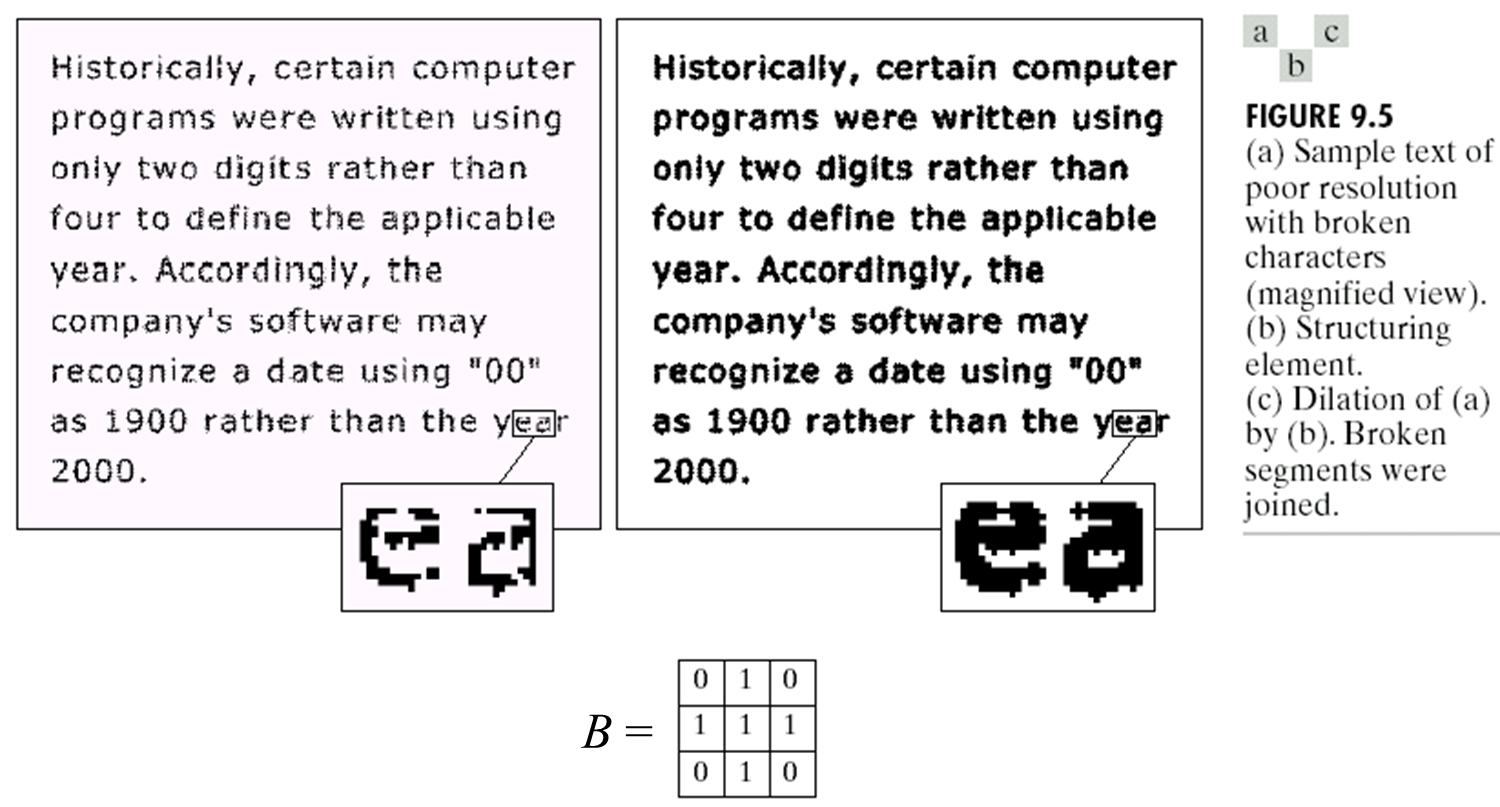
从上图可以看出膨胀可以用来加粗字体，也使得一些断掉的地方连接起来了。下面是腐蚀和膨胀的对比：

侵蚀实际上就是背景的膨胀，但是要注意，膨胀不是侵蚀的逆，也就是你侵蚀然后膨胀，不一定得到原来的结果。

使用不同形状的SE也能得到不同的结果：

下面这张图，使用一个交叉形状的SE进行腐蚀操作，来定位这个网格在哪里断掉了：

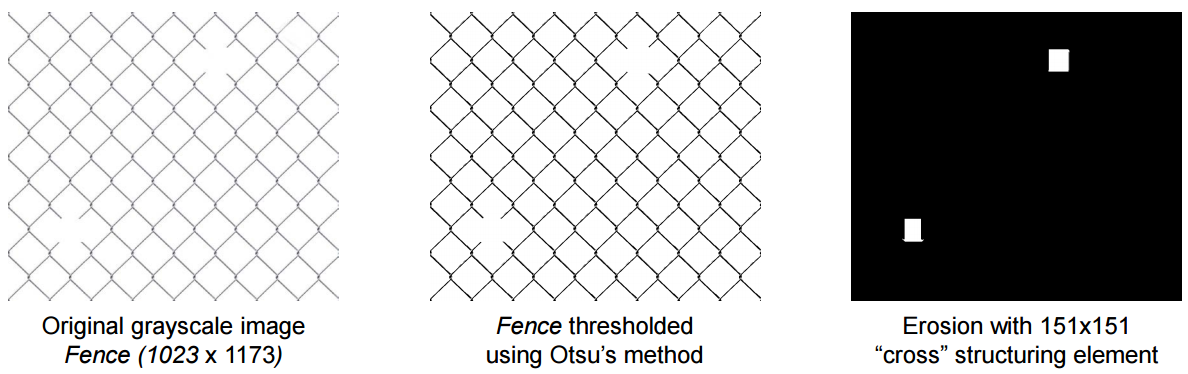
开闭（Opening & Closing）

开闭操作实际上是侵蚀和膨胀的组合。Opening操作先腐蚀然后膨胀，一般来说可以用来平滑一个物体，如下图：

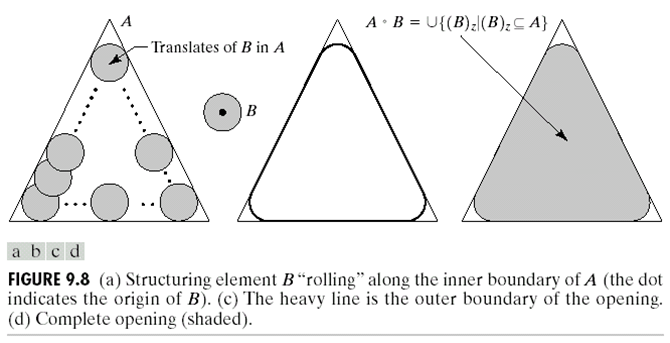
需要注意的是，这里使用了圆形的SE，而矩形的SE会得到不同的形状。Opening操作定义如下： \[ A \circ B = (A \ominus B) \oplus B \] Opening有下面几个性质:

• \(A \circ B \subset A\)
• \((A \circ B) \circ B = A \circ B\)

Closing操作只是顺序与Opening不同： \[ A \bullet B = (A \oplus B) \ominus B \]

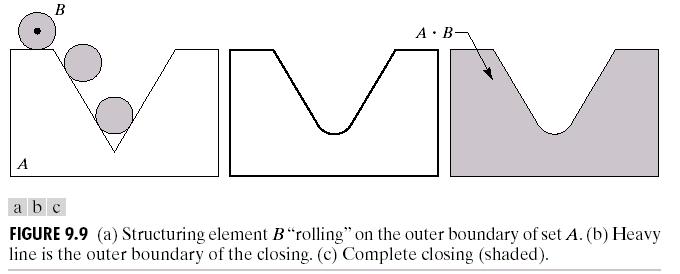
它具有下面的性质：

• \(A \subset (A \bullet B)\)
• \((A \bullet B) \bullet B = A \bullet B\)

Opening与Closing是对偶操作： \[ (A \bullet B)^c = A^c \circ \hat B \] 下面一张图展现了开闭操作的对比：

可以看到Opening可以使得细微的链接断裂，而Closing一般会填补更小的空洞缝隙等，他们都可以平滑对象。

下面这张图展示了Opening，closing操作在指纹上的应用：

边界提取

之前也介绍了一些边界提取的算法，主要使用的是滤波器。这次我们介绍形态学图像处理中如何对二值化的图像进行边界处理。

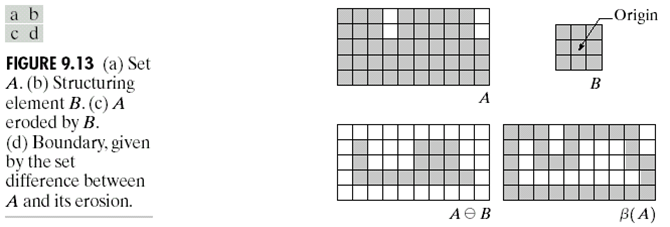
\(\beta (A)\)表示了一个集合\(A\)的边界，那么我们可以通过下面的操作来提取边界： \[ \beta (A ) = A - (A \ominus B). \] 这个道理很简单，就是用原来的图像减去了被腐蚀的图像，因为腐蚀一定会将边界腐蚀掉，下图是一个直观解释：

区域填充

区域填充可以用来一个边界，或者空洞。算法如下： \[ X_k = (X_{k-1} \oplus B) \cap A^c,k = 1,2,3,X_0 = p \] 这里的p是待填充区域中的一个点，而B是一个对称的SE。这里与\(A^c\)求交集，保证了得到的点都在待处理的区域内部，而不会逃出边界。当\(X_k =X_{k-1}\)时，算法停止，下面是这个算法的运行过程：

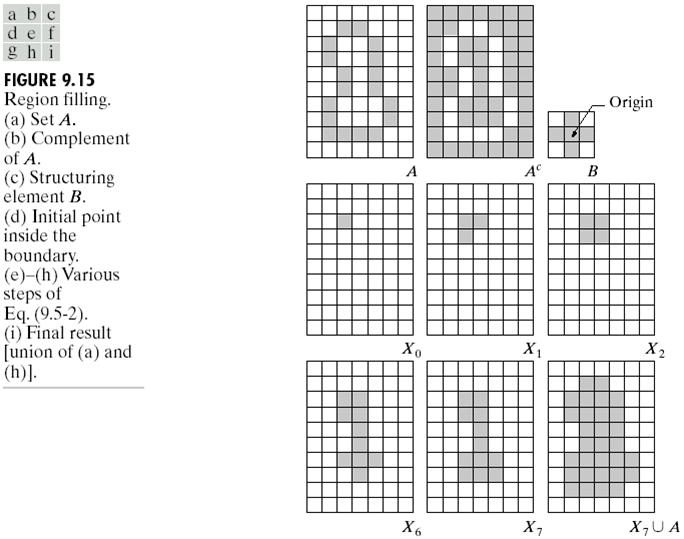
这个算法的运行原理也很简单，首先是膨胀一个待填充区域的点，膨胀之后将该点以及SE与原图像的补集做交集，实际上这样得到的就是接下来需要膨胀的点。一直这样操作，直到最终算法停止。下面是区域填充算法的效果：

骨架提取

对于姿势模拟，骨架提取是非常重要的。骨架\(S(A)\)定义如下：对于一个点\(z\)，定义\((D)_z\)是最大的以\(z\)为中心的一个圆盘，并且被A完全包含。如果\((D)_z\)接触了\(A\)的边界两个点以上，而且没有办法找到比\((D)_z\)更大的圆盘（不局限于以z为中心），那么\((D)_z\)被称为最大圆盘，而这个\(z\)正是骨架上的一点，所有的这样的\(z\)构成了骨架。

实际上骨架的定义直观来说很容易明白，但是努力用数学语言描述反而说得复杂了。下面是骨架的示意图：

骨架提取算法如下： \[ S(A) = \bigcup_{k=0}^K S_k(A) \] 其中: \[ S_k(A) = (A \ominus k B) - (A \ominus kB) \circ B\\ (A \ominus kB) = (...((A \ominus B) \ominus B )...)\ominus B \] 可以看到\((A \ominus kB)\)也就是不断地对A进行腐蚀。而\(K\)被定义为将\(A\)腐蚀为空集的腐蚀次数： \[ K = \max \{k \vert (A \ominus kB) \ne \emptyset \}. \] 算法首先将\(A\)进行腐蚀，这是合理的，但是这样得到的并不一定是骨架，可能还是相对膨胀的，因此这里还加了减去开操作。开操作使用不同的SE可以得到不同的效果，但是平滑明显不是这里使用它的主要原因。腐蚀可能直接将细微的连接直接腐蚀了，而增加开操作可以除掉这些细微的连接，同时对于大片的区域会保存下来，因此用原图减去开操作可以比较好的保留下来这个细微的连接。每次都这样，首先尝试把物体变细，然后保存细微的连接，然后将这些连接取并集，就可以得到骨架。当然，这里的骨架提取是非常简单的，而且不一定会连续，实际上还有很多更高级的骨架提取算法，可以查阅相关的论文。

我们也可以通过骨架来尝试重建原来的图形，但是很大可能不会和原来一样了。重建算法如下： \[ A = \bigcup _{k=0}^K (S_k(A) \oplus kB)\\ (S_k(A) \oplus kB) = (...((S_k(A) \oplus B) \oplus B) \oplus... )\oplus B \] 因此，也就是一个不断膨胀的过程。下面是算法的简单示意图：

这里的形态学图像处理，目前看起来很基础，不知道有什么用，但是实际上简单的规则可以构成非常复杂庞大的系统。这里有一份关于形态学图像处理的补充材料，如果感兴趣可以阅读，看看形态学图像处理可以做那些神奇的事情：Supplementary Material。