数字图像处理——频域滤波

Posted on 2019-04-29 Edited on 2023-10-22 In 数字图像处理

空间域的算法很多，也容易理解，但是有时候却很难设计。而有时候一些问题，转化到频域上，就变得迎刃而解了。

从空间域到频域，不得不提的是傅里叶变换(一般信号处理上，从时域到频域)。这里首先说明下什么是变换，也就是将原有的函数，转换成另外的一些更容易分析的函数之和。变换给了我们不同看事物的角度。比较有名的变换有傅里叶变换，拉普拉斯变换，小波变换等等。

傅里叶变换

我们这里主要用到的是傅里叶变换。傅里叶变换的原始定义如下： \[ f(t) \rightarrow F(\omega)=\int f(t) e^{-j \omega t} d t \] 这里的$t, \omega$可以是标量，也可以是向量。

如果值是离散的，那么有离散傅里叶变化（DFT，Discrete Fourier Transformation）。离散傅里叶变换和连续傅里叶变化形式上差距还是挺大的： \[ F(u)=\sum_{x=0}^{N-1} f(x) \cdot e^{-i \frac{2 \pi}{M} x u} \] 从矩阵视角： \[ \begin{array}{c}{\vec{v}=A \vec{u} } \\ {\vec{u}=[u(0), u[1], \cdots, u(N-1)]^{T}, \vec{v}=[v(0), v[1], \cdots, v(N-1)]^{T} } \\ {A=[a(I, m)]_{N \times N}, \text { where } a(l, m)=\frac{1}{\sqrt{N} } e^{-j \frac{2 \pi}{N}(l-1)(m-1)} }\end{array} \] 为什么长这个样子，离散傅里叶变换背后的数学推倒是比较复杂的，幸运的是我们也不需要了解太多，因此在这里就不多说了。这里$A$矩阵是酋矩阵（unitary matrix）：

$A^{-1}=A^{* T}=A^{H}.$

有了这个，IDFT（离散傅里叶逆变换）就很容易计算了。因为： \[ \begin{aligned} u &=A^{-1} v \\ u &=A^{H} v \\ \Rightarrow u[n] &=\sum_{k=0}^{N-1} v[k] a^{*}(k, n) \end{aligned} \] 这里，$v(k)$是加权系数，而$a^{*}(k, n)$为基函数。

上面提到的是一维的DFT，对于二维的DFT会更麻烦一点。

原始的图像我们用U表示，如下： \[ U=\{u[m, n], 0 \leq m, n \leq N-1\} \] 转换系数： \[ v[k, l]=\sum_{m=0}^{N-1} \sum_{n=0}^{N-1} u[m, n] a_{k l}[m, n] \] 因为A是酋矩阵： \[ u[m, n]=\sum_{k=0}^{N-1} \sum_{l=0}^{N-1} v[k, l] a_{k /}^{*}[m, n] \] 基函数$a_{kl}[m,n]$以及$a_{kl}^*[m,n]$满足：

特殊域正交： \[\sum_{m=0}^{N-1} \sum_{n=0}^{N-1} a_{k l}[m, n] a_{k^{\prime} / l}^{*}[m, n]=\delta\left[k-k^{\prime}, I-l^{\prime}\right]\]
空间域的完备性： \[\sum_{k=0}^{N-1} \sum_{l=0}^{N-1} a_{k l}[m, n] a_{k l}^{*}\left[m^{\prime}, n^{\prime}\right]=\delta\left[m-m^{\prime}, n-n^{\prime}\right]\]

可以看到这里任何一个系数估计都是全局计算，需要$N^2$个乘法以及$N^2-1$个加法。而所有系数计算需要$N^4$的复杂度。这个复杂度是难以接受的。因此我们需要快速傅里叶变换（FFT），对于快速傅里叶变换的具体算法这里就不多介绍了，但是它已经被嵌入到各种各样的程序包中了，可以随时调用。

常见的傅里叶变换

为了介绍离散傅里叶变换的性质，我们先认识下面一些函数：

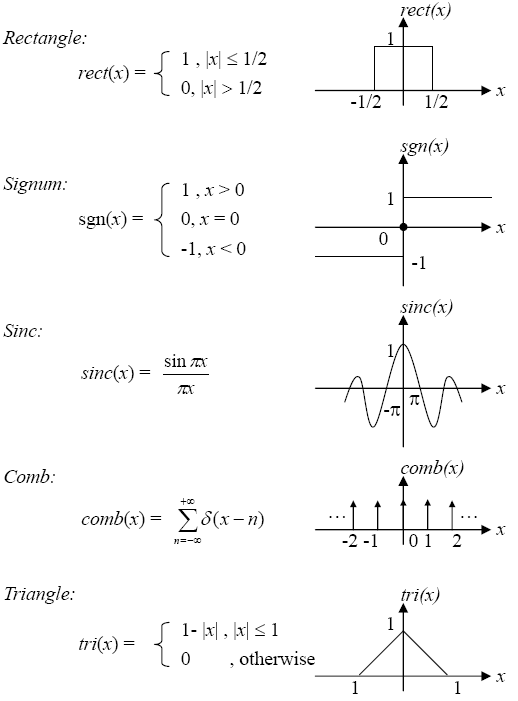
对于傅里叶变换：$f(x,y) \rightarrow F(x,y)$，那么一些常见的函数的傅里叶变换有（$\delta(x, y )$为冲激函数）：

$f(x,y)$	$F(x,y)$
$\delta(x, y)$	$1$
$\delta\left(x \pm x_{0}, y \pm y_{0}\right)$	$e^{ \pm j 2 \pi\left(x_{0} \xi_{1}+y_{0} \xi_{2}\right)}$
$e^{-\pi\left(x^{2}+y^{2}\right)}$	$e^{-\pi\left(\xi_{1}^{2}+\xi_{2}^{2}\right)}$
$\operatorname{rect}(x, y)=\operatorname{rect}(x) \operatorname{rect}(y)$	$\operatorname{sinc}\left(\xi_{1}, \xi_{2}\right)=\operatorname{sinc}\left(\xi_{1}\right) \operatorname{sinc}\left(\xi_{2}\right)$
$\operatorname{tri}(x, y)$	$\sin c^{2}\left(\xi_{1}, \xi_{2}\right)$
$\operatorname{comb}(x, y)$	$\operatorname{comb}\left(\xi_{1}, \xi_{2}\right)$

Translation

${f(x, y) \rightarrow F(u, v)}$
${f(x, y) e^{\left(j u_{0} x+j v_{0} y\right)} \rightarrow F\left(u-u_{0}, v-v_{0}\right)}$
${f\left(x-x_{0}, y-y_{0}\right) \rightarrow F(u, v) e^{\left(-j u x_{0}-j y_{0}\right)} }$

Multiplication and Convolution

${f(x, y) g(x, y) F(u, v) G(u, v)} $
${f(x, y) g(x, y) F(u, v) G(u, v)} $

Scaling

f(a t) F(), a , a

对于傅里叶，必须要提的是高斯函数。它有很多优秀的性质：

在空间和频域上都有一定的跨度。
高斯的傅里叶变换依然是高斯函数
高斯函数乘以高斯函数还是一个高斯函数，只是标准差不同
高斯函数的标准差是一个尺度参数
我们经常需要在不同尺度上观察图片，而高斯金字塔是一个很好的工具

高斯金字塔是著名的SIFT特征必不可少的预处理步骤。不同尺寸的高斯金字塔，模拟了场景离我们眼睛越来越远时候看到的效果，想对高斯金字塔有详细了解的可以参考论文：Gaussian Pyramid.

频域滤波

在频域上滤波，能够多个看图片的视角，也很容易设计滤波器的形状。它的缺点是计算量较大，由于数字化，使得算法也较为复杂，比如上面的傅里叶变换，我就没完全理解。但是有一些问题，在频域下就非常直观。比如下图：

可以看到原图的去噪（很有规律）在空间域上是几乎无法去除的，但是在频域上就可以看出，是多余的一些异常点造成了这样的噪声。频域滤波的一般过程如下：

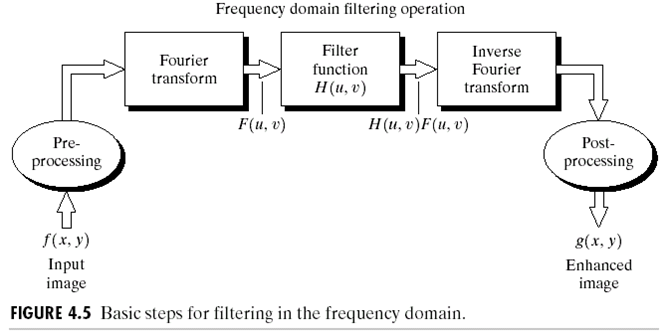
在空间域上的卷积，对应着频域的乘积，因此频域中使用的是乘积操作。频域上一般有高通滤波，低通滤波以及带通滤波。

下面是一张图片的原始图和频域图：

低通滤波

低通滤波可以用来平滑或者模糊图像。关于低通滤波，这里介绍三种滤波器，理想的低通滤波，巴特沃斯滤波，高斯低通滤波。它们都是各向同性的，它们之间的关系是：

理想的低通滤波数学形式如下： \[ H(u, v)=\left\{\begin{array}{ll}{1} & {\text { if } D(u, v) \leq D_{0} } \\ {0} & {\text { if } D(u, v)>D_{0} }\end{array}\right. \] $D(u, v )$代表的是到原点的欧几里得距离，低通滤波如下图：

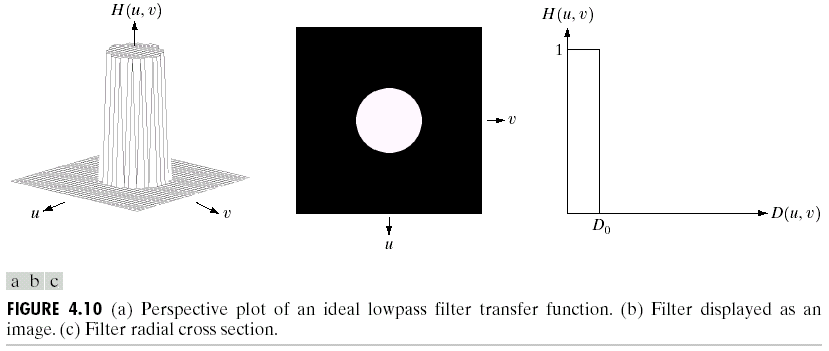
这里$D_0$是截断频率，如果确定截断频率是非常重要的一件事，它和我们想滤掉多少频分以及图像的分布有关。下面是一个低通滤波的例子：

低通滤波很明显可以模糊图像，但是它会带来振铃效应（ringing effect）:

高斯低通滤波（Gaussian Low-Pass Filter）的做法是用$D_0$代替高斯滤波中的$\delta$： \[ H(u, v)=e^{-\frac{D^{2}(u, v)}{2 D_{0}^{2} } } \]

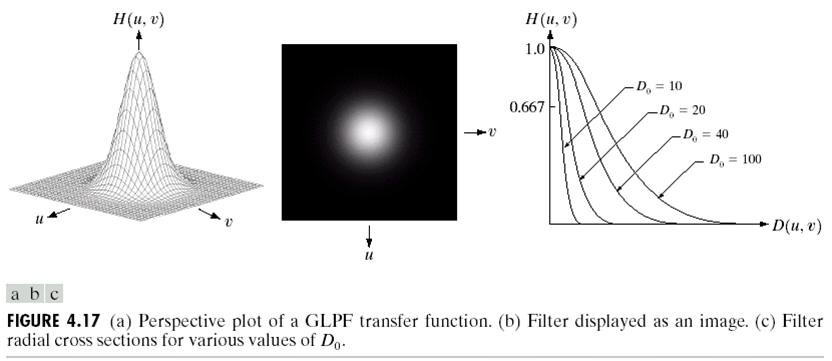
高斯低通滤波的好处在于它在空间域内也容易得到解析形式，而不需要傅里叶变换，而且与理想的低通滤波器相比，在空间域它没有振铃效应。

但是高斯低通滤波的缺点是有时候它不够sharp。因为我们知道，理想低通滤波是直接截断，而高斯滤波则是有比较缓慢的过渡过程。

巴特沃斯低通滤波(Butterworth Low-Pass Filter), 是介于低通滤波与高斯滤波中间的滤波器。它的数学形式如下： \[ H(u, v)=\frac{1}{1+\left[\frac{D(u, v)}{D_{0} }\right]^{2 n} } \]

它的振铃效应和次数n有关。

效果图如下：

高通滤波

有时候我们需要锐化特征的滤波器，高通滤波可以做到这一点。类似于低通滤波，它也有三种类型，理想高通滤波（Ideal High Pass Filter），高斯高通滤波（Gaussian High Pass Filter）以及巴特沃斯高通滤波（Butterworth High Pass）。

理想高通滤波数学形式： \[ H(u, v)=\left\{\begin{array}{ll}{0} & {\text { if } D(u, v) \leq D_{0} } \\ {1} & {\text { if } D(u, v)>D_{0} }\end{array}\right. \] 高斯高通滤波数学形式： \[ H(u, v)=1-e^{-\frac{D^{2}(u, v)}{2 D_{0}^{2} } } \] 巴特沃斯高通滤波数学形式： \[ H(u, v)=\frac{1}{1+\left[\frac{D_{0} }{D(u, v)}\right]^{2 n} } \] 下图分别是IHPF，GHPF，BHPF的图像：

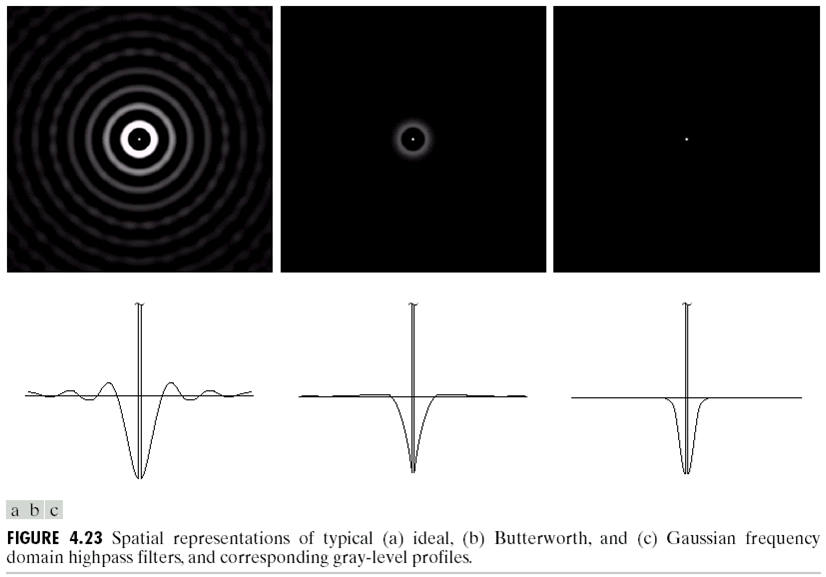
滤波效果：

空间域和频域

在空间域的滤波可以转换成设计在频域的滤波，比如拉普拉斯算子。在空间域中，它的推导如下： \[ \begin{aligned} \nabla^{2} f &=\frac{\partial^{2} f}{\partial x^{2} }+\frac{\partial^{2} f}{\partial y^{2} } \\ \frac{\partial^{2} f}{\partial x^{2} } &=f(x+1, y)+f(x-1, y)-2 f(x, y) \\ \frac{\partial^{2} f}{\partial y^{2} } &=f(x, y+1)+f(x, y-1)-2 f(x, y) \\ \nabla^{2} f &=[f(x+1, y)+f(x-1, y)+f(x, y+1)+f(x, y-1)]-4 f(x, y) \end{aligned} \] 由此得到下面的滤波器：

而在频域中，我们可以计算： \[ \begin{aligned} \mathfrak{F}\left[\frac{d^{n} f(x)}{d x^{n} }\right] &=(j u)^{n} F(u) \\ \widetilde{\mathfrak{F} }\left[\frac{\partial^{2} f(x, y)}{\partial x^{2} }+\frac{\partial^{2} f(x, y)}{\partial y^{2} }\right] &=(j u)^{2} F(u, v)+(j v)^{2} F(u, v) \\ &=-\left(u^{2}+v^{2}\right) F(u, v) \\ \mathfrak{F}\left[\nabla^{2} f(x, y)\right] &=-\left(u^{2}+v^{2}\right) F(u, v) \end{aligned} \] 因此在频域中，滤波器形状为：\[H(u, v)=-\left(u^{2}+v^{2}\right)\].

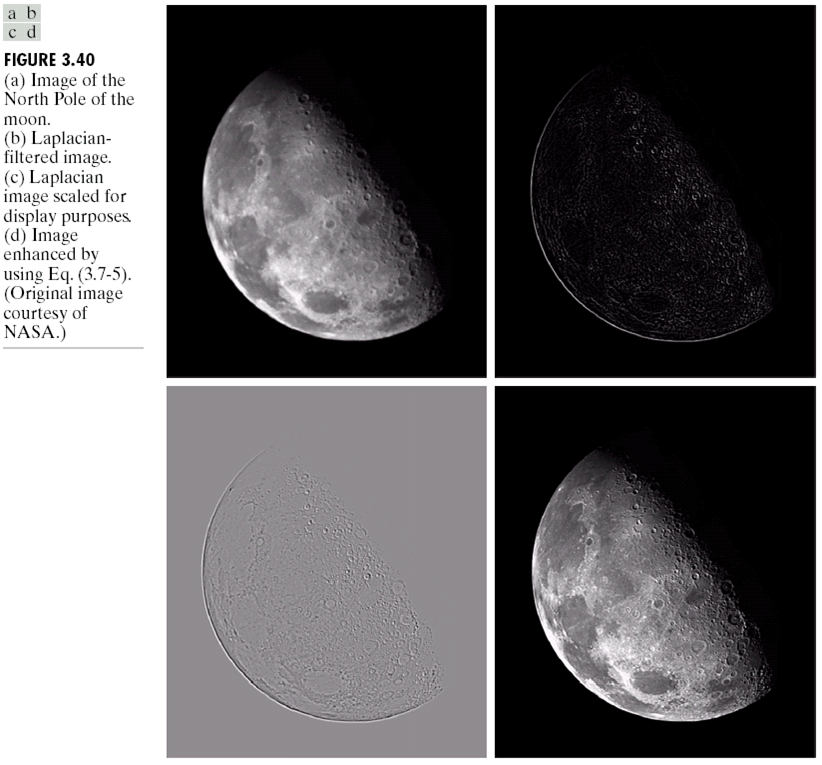
在之前，我们介绍到锐化特征时候的做法，就是先通过原图与模糊图相减得到边缘，然后再加到原始图像上。使用拉普拉斯算子也可以这样做，将使用拉普拉斯算子滤波后的图加到原始图像上，可以得到锐化的效果。数学形式如下： \[ g(x, y)=\left\{\begin{array}{ll}{f(x, y)-\nabla^{2} f(x, y)} & {\text { if the center coefficient of the Laplacian mask is negative} } \\ {f(x, y)+\nabla^{2} f(x, y)} & {\text { if the center coefficient of the Laplacian mask is positive.} }\end{array}\right. \] 效果如图：

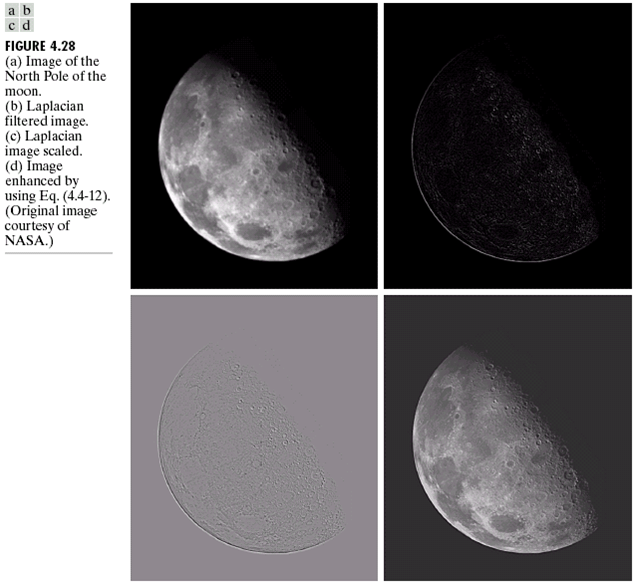
在频域上我们这样做，也可以实现锐化的效果：

在空间域上，我们做非锐化屏蔽（unsharp masking）是这样的： \[ f_{\mathrm{hp} }(x, y)=f(x, y)-f_{\mathrm{lp} }(x, y) \] 在频域上，需要下面这样做： \[ F_{\mathrm{hp} }(u, v)=F(u, v)-F_{\mathrm{lp} }(u, v) \] 因为$F_{\mathrm{lp} }(u, v)=H_{\mathrm{lp} }(u, v) F(u, v)$，所以我们得到： \[ H_{\mathrm{hp} }(u, v)=1-H_{\mathrm{lp} }(u, v) \] 一般来说，空间域易于计算，频域更容易理解和设计算法，但是相对复杂，计算量也较大，DFT是实现频域算法的关键步骤。

其他一些频域滤波

高通量滤波

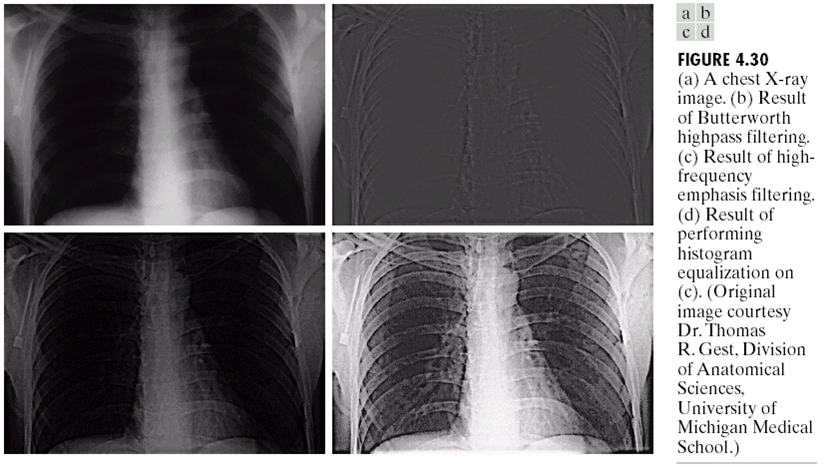
上一篇文章介绍了，在空间域中，高通量滤波（High-boosting filtering）的做法，首先计算非锐化屏蔽（unsharp masking）的图： \[ f_{s}(x, y)=f(x, y)-\overline{f}(x, y) \] 然后让原图加上计算的图（这里的A可能和之前的k相关）： \[ \begin{aligned} f_{\mathrm{hb} }(x, y) &=A f(x, y)-\overline{f}(x, y) \\ f_{\mathrm{hb} }(x, y) &=(A-1) f(x, y)+f(x, y)-\overline{f}(x, y) \\ f_{\mathrm{hb} }(x, y) &=(A-1) f(x, y)+f_{s}(x, y) \end{aligned} \] 而在频域上的高通量滤波如下： \[ H_{\mathrm{hb} }(u, v)=(A-1)+H_{\mathrm{hp} }(u, v) \] ### 高频强调滤波

除了高通量滤波，这里再介绍一个类似于高通量滤波的滤波器：高频强调滤波（High-Frequency Emphasis Filtering）。它可以增强高频成分。数学形式如下： \[ H_{\mathrm{hfe} }(u, v)=a+b H_{\mathrm{hp} }(u, v) \] 可以看到的是，当上式中$a = (A-1),b=1$时，它与高通量滤波一致。一般来说这里的$b$会大于1，可以强调高频的成分。

同态滤波

同态滤波（Homomorphic Filtering）想法来源于illumination-reflectance模型： \[ f(x, y)=i(x, y) r(x, y) \] 但是在频域上是很难实现的，因为空间域中的乘积意味着频域中的卷积。解决方法是，在转化到频域之前，先利用log函数，然后经过滤波之后回到空间域，再使用log的逆达到想要的效果。流程如下：

同态滤波应用在于减少光照变化并且锐化边缘，它可以减少低频增加高频。因为显示中光照变化缓慢，属于低频，而反射变化比较突然，属于高频信息。同态滤波的函数曲线应该如下图，低频的信息给较低的权重，而高频的信息给较高的权重。

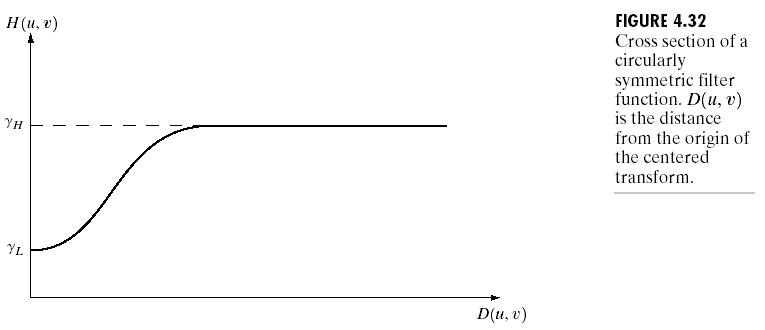
下面是同态滤波效果图：

实现上图的效果的滤波器数学形式如下： \[ \begin{array}{l}{H(u, v)=\left(\gamma_{H}-\gamma_{L}\right)\left[1-e^{-c\left(\frac{D^{2}(u, y)}{D_{0}^{2} }\right)}\right]+\gamma_{L} } \\ {\text { where } \gamma_{L}=0.5, \gamma_{H}=2.0}\end{array} \] 实现中一些值得注意的问题 -------------------------------------------------------------------------------------------------------------------------------------------------------

FS，FT，DFT

对于不同的信号，空间域中，非周期的连续信号，使用FT，周期连续信号，使用FT，FS（傅里叶级数），周期离散信号，使用DFT。而使用DFT时，我们暗示假设了周期性，因此总是会使用循环卷积。

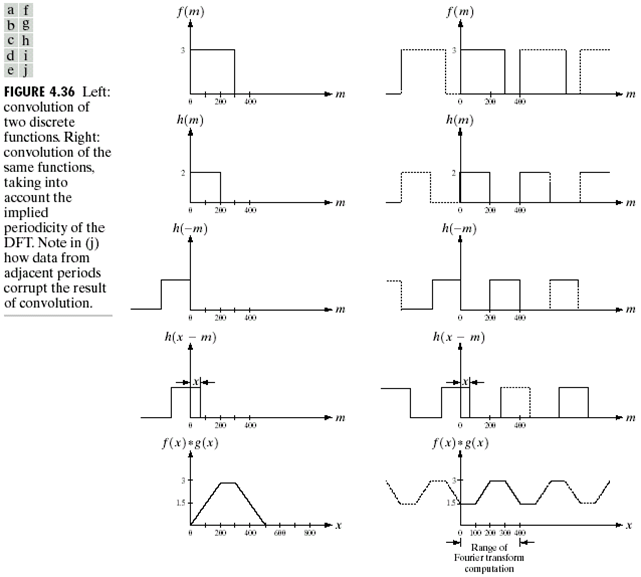
Zero padding

补零操作细节如下： \[ f_{e}(x)=\left\{\begin{array}{ll}{f(x)} & {0 \leq x \leq A-1} \\ {0} & {A \leq x \leq P}\end{array}\right. g_{e}(x)=\left\{\begin{array}{ll}{g(x)} & {0 \leq x \leq B-1} \\ {0} & {B \leq x \leq P}\end{array}\right. \] 上式中，$P\ge A +B - 1$。

DC component

DFT中直流分量占据了大量的位置，一般来说，我们会把直流分量放在图的中间。如果实现这个？在matlab中使用fftshift，它利用了DFT的性质： \[ f\left(x-x_{0}, y-y_{0}\right) \longleftrightarrow F(u, v) e^{-j 2 \pi\left(u \frac{x_{0} }{M}+v \frac{y_{0} }{N}\right)} \] 当$x_0=\frac{M}{2},y_0=\frac{N}{2}$： \[ f\left(x-\frac{M}{2}, y-\frac{N}{2}\right) \longleftrightarrow F(u, v)(-1)^{(u+v)} \] 类似的： \[ f(x, y) e^{j 2 \pi\left(u \frac{x_{0} }{M}+v \frac{y_{0} }{N}\right)} \longleftrightarrow F\left(u-u_{0}, v-v_{0}\right) \] 当$u_0=\frac{M}{2},v_0 = \frac{N}{2}$， \[ f(x, y)(-1)^{(x+y)} \longleftrightarrow F\left(u-\frac{M}{2}, v-\frac{N}{2}\right) \]

\(f(x,y)\)	\(F(x,y)\)
\(\delta(x, y)\)	\(1\)
\(\delta\left(x \pm x_{0}, y \pm y_{0}\right)\)	\(e^{ \pm j 2 \pi\left(x_{0} \xi_{1}+y_{0} \xi_{2}\right)}\)
\(e^{-\pi\left(x^{2}+y^{2}\right)}\)	\(e^{-\pi\left(\xi_{1}^{2}+\xi_{2}^{2}\right)}\)
\(\operatorname{rect}(x, y)=\operatorname{rect}(x) \operatorname{rect}(y)\)	\(\operatorname{sinc}\left(\xi_{1}, \xi_{2}\right)=\operatorname{sinc}\left(\xi_{1}\right) \operatorname{sinc}\left(\xi_{2}\right)\)
\(\operatorname{tri}(x, y)\)	\(\sin c^{2}\left(\xi_{1}, \xi_{2}\right)\)
\(\operatorname{comb}(x, y)\)	\(\operatorname{comb}\left(\xi_{1}, \xi_{2}\right)\)