图形学——B样条曲线和曲面

Posted on 2019-03-19 Edited on 2023-10-22 In 图形学

Bezier曲线虽然有很多优点，但是有一些明显的缺点。上次也提到了，在CAD中通常不鼓励使用高阶的Bezier基函数来画曲线，而使用低阶拼接。但是在低阶中拼接，要保证几何连续性又是非常困难的一件事情。对于Bezier曲线，如果控制点过多，无法进行局部调控。改变一个控制点，就会改变整个曲线，这里介绍B样条。

B样条的动机来源于插值中的Runge-Kutta现象，高阶多项式很容易产生不稳定的上下波动。而样条思想，就是用分段低阶多项式通过连续的连接来代替高阶的多项式。

引出B样条

在Schoenberg提出了一个基于样条的方法来近似曲线，在提出之后的很长一段时间里，人们都认为使用样条来进行形状设计太过于复杂，因此不能实现，直到Gordon和Riesenfeld基于前人的工作提出了B样条以及一系列对应的几何算法。B样条曲线和曲面保证了Bezier的优点，同时也克服了Bezier曲线的缺点。

样条函数的插值，可以通过求解一个三对角方程来进行，可能就是对几个点做一个空间曲线（比如二次三次）的假设，求解曲线的参数。而对于一个给定的区间划分，可以类似地计算样条曲线的插值。给定区间上的所有样条函数组成一个线性空间，这个线性空间的基函数就叫做B样条基函数。

B样条曲线及其性质

\[ P(t) = \sum_{i=0}^nP_iN_{i,k}(t). \] 上式中，$P_{i}(i=0,…,n)$是控制点，$N_{i,k}(i=0,…,n)$是第$i$个$k$阶B样条基函数。B样条基函数是分段$k$次（$k+1$阶）多项式，它们由节点向量唯一决定，节点向量则是一串非减的实数序列。要注意这里的阶比次多一，但是实际上是一样的，只是由于历史原因叫法不同。次是从0开始，而阶从1开始。

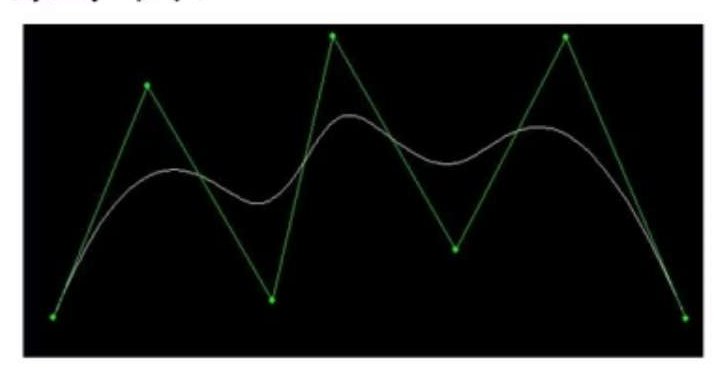
B样条基函数定义有多种解释，最简单的是由de Boor-Cox递推公式定义的： \[ N_{i,0}(t) = \left\{\begin{matrix} 1 & t_i < t< t_{i+1}\\ 0 & otherwise \end{matrix}\right.\\ N_{i,k} = \frac{t - t_i}{t_{i+k} - t_{i} }N_{i,k-1}(t) + \frac{t_{i+k+1} - t}{t_{i+k+1} - t_{i+1} } N_{i+1,k-1}(t) \] 而$t$为节点向量，非减的实数序列： \[ t_0,t_1,...,t_{k-1},t_k,...,t_n,t_{n+1},...,t_{n+k-1},t_{n+k+1}. \] 现在考虑几个B样条基函数的问题：

B样条基函数$N_{i,k}(t)$的非零区间是什么？
从上述可以看到，当$k=0$时，$N_{i,0}(t)$的非零区间为：$(t_i - t_{i+1})$。根据递推公式，可以得到： \[N_{i,1} = \frac{t-t_i}{t_{i+1} - t_{i} } N_{i,0}(t) + \frac{t_{i+2} - t}{t_{i+2}-t_{i+1} }N_{i+1,0}(t)\]

这时候，只要$N_{i,0},N_{i+1,0}$有一个不为0，那么$N_{i,1}$就不为0，因此它的非零区间为：$(t_i,t_{i+1})\cup(t_{i+1},t_{i+2})$,也就是：$(t_{i},t_{i+2})$。

依次类推，我们得到$N_{i,2}$的非零区间为：$(t_i,t_{i+2})\cup(t_{i+1},t_{i+3})$，也就是$(t_{i},t_{i+3})$。

最终得到$N_{i,k}$的非零区间为：$(t_{i},t_{i+k+1})$。

一共需要多少个节点？

$N_{i,k}(t)$的非零区间是$(t_{i},t_{i+k+1})$，共有$n$个控制节点，因此所有的非零区间为：$(t_{0},t_{k+1})\cup (t_{1},t_{k+2})\cup…\cup (t_{n},t_{n+k+1})$。因此需要的节点个数为$n+k+2$。

B样条插值得到的曲线定义区间是什么？
这个也很容易得到：$(0,t_{n+k+1})$。

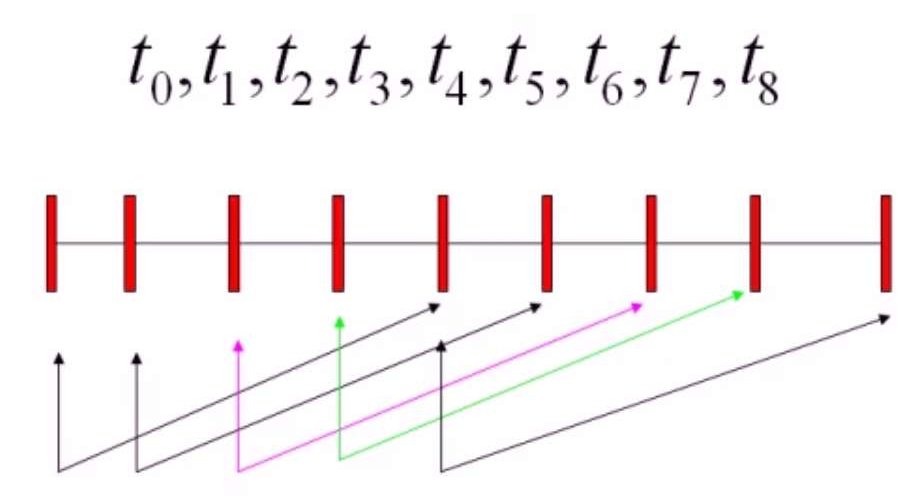
以$k=3,n=4$为例：$P_{t} = \sum_{i=0}^4P_iN_{i,3}(t)$，则求解$N_{i,3}$的过程如下图：

B样条基函数性质

B样条基函数有很多性质与Bezier曲线类似。

非负性和局部支撑性
$N_{i,k}(t)$是非负的，$N_{i,k}(t)$是$[t_i,t_{i+k+1}]$上的分段非零多项式：\[ N_{i,k}(t) = \left \{ \begin{matrix} \ge 0 & t\in [t_i,t_{i+k+1}]\\ =0& otherwise \end{matrix} \right.\]
归一性
区间$[t_i,t_{i+1}]$上的所有$k$次非零基函数的和为1： \[ \sum_{i=0}^n N_{i,k}(t) = 1,t \in [t_i,t_{i+1}].\]
基函数所满足的微分方程： \[ N'_{i,k}(t) = \frac{k-1}{t_{i+k-1} - t_i}N_{i,k-1}(t)+\frac{k-1}{t_{i+k}- t_{i+1} }N_{i+1,k-1}(t) \] ### B样条分类

一般的曲线可以根据其起始点和终止点是否重叠分为开曲线（不重叠）和闭曲线（重叠）。

根据节点向量中节点的分类，B样条可以分为：

均匀B样条。节点成等差数列均匀分布，这样的节点分布对应的是均匀B样条基函数。

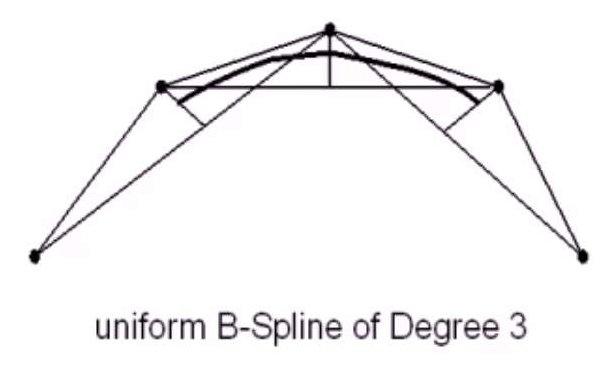
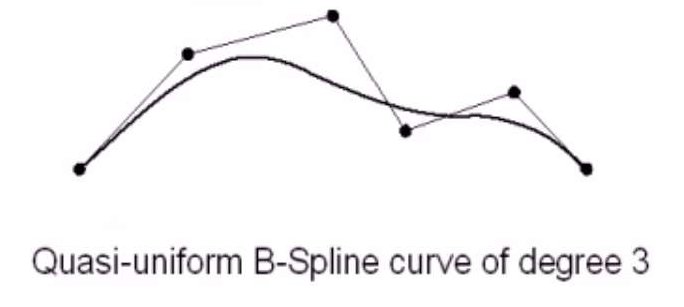
准均匀B样条。准均匀B样条的起始节点和终止节点都具有$k+1$的重复度,其他的节点和均匀B样条一致。均匀B样条不保持Bezier曲线的断电性质，起始点和终止点不在控制端点上。而准均匀B样条具有端点性质。

分段Bezier曲线。
除了终点和起始节点具有k+1个重复度，其他的节点具有$k$个重复度，这样得到的实际上是分段的Bezier曲线。此时需要节点个数满足：$(n+k+2-2)%k=0$。

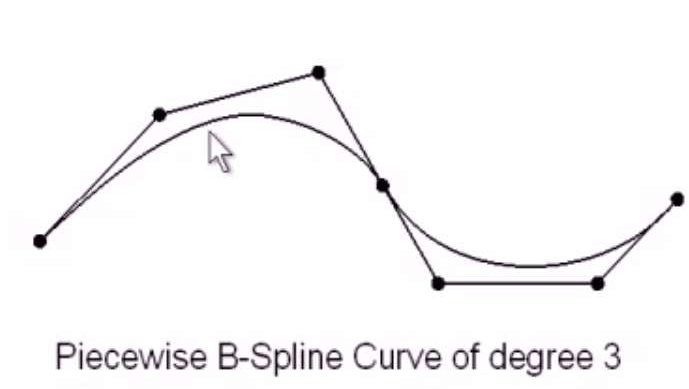
对于分段的Bezier曲线，不同的曲线段相对独立。移动控制点只会影响其所在的Bezier曲线段，而其他的Bezier曲线段不会改变，但是分段Bezier曲线需要更多的参数和变量来进行控制，更多的控制点和更多的节点信息。

非均匀B样条。最一般的B样条，我们主要介绍这个。它的起始节点和终止节点的重复度小于等于$k+1$，而其他节点重复度小于$k$。

非均匀B样条

B样条曲线的性质：

局部支持性。区间$t \in [t_i,t_{i+1}]$上的曲线仅由至多$k+1$个控制点决定。修改控制点$P_i$仅会影响到$(t_i,t_{i+k+1})$上的曲线。

上述这个性质是可以根据定义推导出来的。

连续性：$P(t)$在每一个重复度为$r$的节点上具有$C^{k-r}$的连续性。不知道在说什么。
凸包性。B样条曲线被包围在其控制顶点的凸包内部。
分段多项式性质：任何一个由相邻节点确定的区间上，$P(t)$是一个关于t的次数不超过$k$的多项式。
导数公式： \[\begin{aligned} P'(t) &= \left(\sum_{i=0}^n P_i N_{i,k}(t) \right)' \\ &= \sum_{i = 0}^n P_i N_{i,k}'(t)\\ &= (k-1)\sum_{i=0}^n \left(\frac{P_i - P_{i-1} }{t_{i+k} - t} \right)N_{i,k-1}(t), t\in[t_k,t_{n+1} ] \end{aligned}\]
变差缩减性：任何一条直线与B样条曲线的交点个数不会超过该直线与B样条曲线的控制多边形的交点数目
几何不变性：曲线的形状和相对于控制点的位置不取决于坐标系的选择
仿射不变性：将仿射变换用于控制点，变换后的控制点得到的曲线就是仿射变换后的曲线。
直线保持性：如果控制多边形退化成一条直线，那么B样条曲线在这条直线上
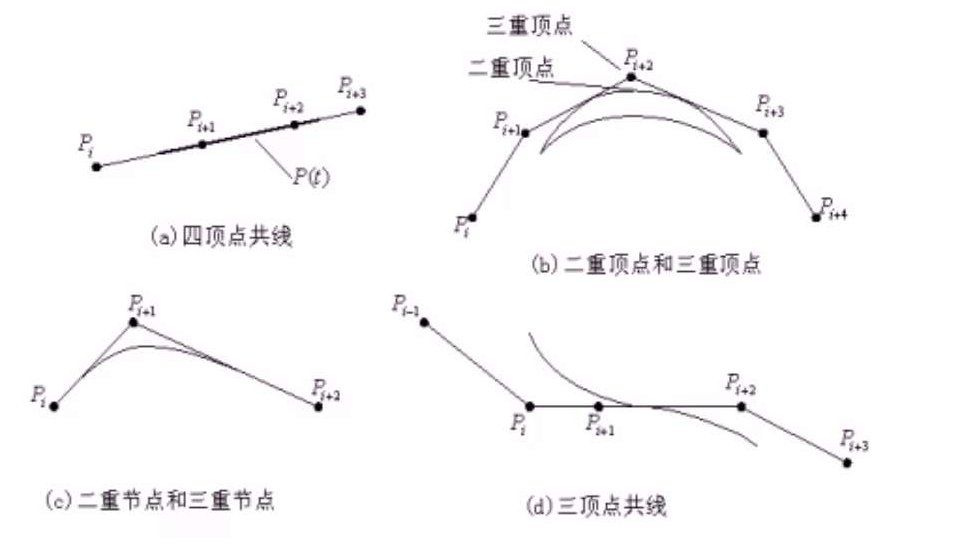
灵活性：使用B样条可以方便构成线段，尖点，切线等等特殊效果。对于灵活性有下面几个3次B样条基函数的例子：

de Boor算法

计算B样条曲线的一点可以直接使用B样条的公式，但是de Boor算法是一个更有效的算法。首先，我们知道： \[ \begin{aligned} P(t) &= \sum_{i=0}^nP_i N_{i,k}(t) = \sum_{i = j-k}^j P_iN_{i,k}(t)\\ &= \sum_{i=j-k}^j P_i \left [\frac{t - t_i}{t_{i + k} - t_i} N_{i,k-1}(t) + \frac{t_{i+k+1} - t}{t_{i + k + 1} - t_{i+1} }N_{i+1,k-1}(t) \right]\\ &= \sum_{i= j-k}^j\left [ \frac{t - t_i}{t_{i+k} - t_i}P_i + \frac{t_{i+k} - t}{t_{i+k} - t_i} P_{i-1} \right] N_{i,k-1}(t) \end{aligned}, t \in [t_j,t_{j+1}] \] 上面式子的由来也就是通过确定$t$的区间段$[t_j,t_{j+1}]$，然后我们知道在这个区间内的曲线最多受到$k+1$个控制顶点的控制。

令： \[ P_i^{[r]}(t) = \left\{ \begin{matrix} P_i& r = 0, i = j-k,..,j;\\ \frac{t - t_i}{t_{i+k+1-r} - t_i}P_i^{[r-1]}(t) + \frac{t_{i+k+1-r} - t}{t_{i+k+1-r} - t_i} P_{i-1}^{[r-1]}(t)& r = 1,2,...,k-1; i = j-k+r,...,j \end{matrix} \right. \] 则： \[ \begin{aligned} P(t) &= \sum_{i=j-k}^jP_iN_{i,k}(t)\\ &= \sum_{i= j -k+ 1}^j P_i^{[1]}(t)N_{i,k}(t) \\ &= \sum_{i=j-k+2}^jP_i^{[2]}(t)N_{i,k-2}(t)\\ &= ...\\ &= P_i^{[k]}(t)N_{i,0}(t) \end{aligned} \] 这就是de Boor算法。de Boor算法的递推也就是$P_i^{[k]}(t)$的过程。为了求这个，需要的递归方式如下图（下图的k表示的是阶数，因此是从$j-k+1$到$j$，需要的是$k$个控制点点，也就是次数里$k+1$个控制点）：

对于de Boor算法有比较直观的几何解释，也就是割角。因此它也被称为割角算法。下图的k依然是阶数。

节点插入

节点插入可以增加曲线的可控度。为了增加节点而且保持原有的曲线形状以及原来的次数，需要改变控制顶点的个数。节点插入可以被描述为下面的过程：

插入新的节点$t$到节点区间$[t_i,t_{i+1}]$
节点向量变为：$T^1 = [t_0,t_1,…,t_i,t,t_{i+1},…,t_{n+k+1}]$
新的节点向量变为：$T^1 = [t^1_0,…,t^1_i,t^1_{i+1},t^1_{i+2},…,t_{n+k+2}]$

新的节点向量对应了新的B样条计函数。假设原始曲线$P(t)$可以由这些新的基函数和新的控制定点$P_j^1$来表示，则： \[ P(t) = \sum_{j=0}^{n+1}P_j^1 N^1_{j,k}(t) \] 而Boehm给出了计算这些新的控制点的公式： \[ \left\{ \begin{matrix} P_j^1 = P_j & j=0,1,...,i-k\\ P_j^1 = (1 - \beta_j)P_{j-1}+\beta_jP_j& j = i-k+1,...,i-r\\ P_j^1 = P_{j-1} & j=i-r+1,...,n+1 \end{matrix} \right. \] 上式中： \[ \beta_j = \frac{t - t_j}{t_{j+k} - t_j}, \] $r$是新插入的节点$t$在节点序列中的重复度。如下图（图中k为阶数）：

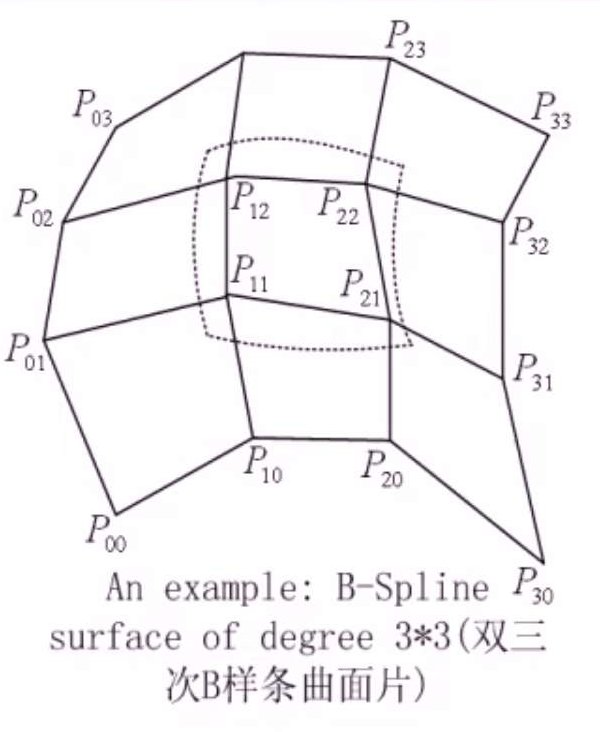
B样条曲面

给定$U,V$轴上的节点向量： \[ U = [u_0,u_1,...,u_{m+p}]\\ V = [v_0,v_1,...,v_{n+q}] \] 阶为$p \times q$的B样条曲面可以定义为： \[ P(u,v) = \sum_{i=0}^m \sum_{j=0}^n P_{ij}N_{i,p}(u)N_{j,q}(v) \]

NURBS曲线/曲面

B样条和Bezier都有缺点，不能精确表示圆锥曲线。而NURBS（非均匀有理B样条）目的在于找到能精确描述圆锥曲线以及二次曲面的方法。在这里简单介绍一下NURBS。

NURBS有下面几个优势：

它提供了一个更一般更精确的方法来表达并对自由曲线/曲面进行设计。
提供了一个通用的数学形式，可以同时表示标准的解析曲线/曲面（如圆锥曲线）以及自由曲线/曲面（如参数曲线）。
存在稳定快速的数值计算方法。
具有仿射变换不变性，也有投影变换不变性
对于NURBS的控制点和权重都能任意修改，用NURBS来做设计有更大的灵活性
非有理B样条，非有理和有理Bezier曲线/曲面都可以看作NURBS的特殊形式
它的缺点是比传统的表达需要更大的存储空间，而且如果权重设计不合理，NURBS曲线可能会产生畸变。在某些情况下如曲线重叠，使用NURBS非常难以处理。

NURBS曲线是由分段有理B样条多项式基函数定义的： \[ P(t) = \frac{\sum_{i=0}^n \omega_i P_i N_{i,k}(t)}{\sum_{i=0}^n \omega_iN_{i,k}(t)} = \sum_{i=0}^nP_iR_{i,k}(t) \] 其中： \[ R_{i,k}(t) = \frac{\omega_i N_{i,k}(t)}{\sum_{j=0}^n \omega_jN_{j,k}(t)} \] 因此，从定义可以看出来它是B样条加权重。它的基函数$R_{i,k}(t)$包含了B样条基函数的所有性质：
局部支持性，归一性，可微，变差缩减，凸包，仿射不变。

如果一个控制点的权重为0，那么该控制点的位置不对曲线产生任何影响。

如果一个控制点权重为正无穷，而$\omega_i=+\infty,R_{i,k}(t)=1$，当$t \in [t_i,t_{i+k}$，$P(t) = P_i$。

如果用齐次坐标表示控制点，即：$P_i^{\omega} = (\omega_ix_i,\omega_iy_i,\omega_i)$，则：

P^{} (t) = {i=0}^n P_i^{}N{i,k}(t).

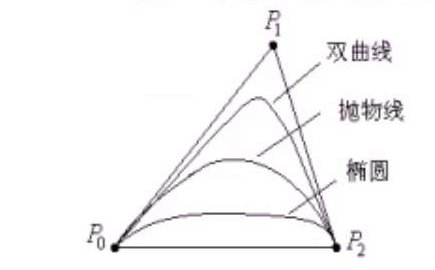
圆锥曲线的NURBS表示

对于3个控制定点，节点向量$T=[0,0,0,1,1,1]$，NURBS曲线退化成二阶Bezier曲线。很容易可以证明该曲线是二次曲线： \[ P(t) = \frac{(1-t^2)\omega_0P_0 + 2t(1-t)\omega_1P_1 + t^2 \omega_2P_2}{(1-t^2)\omega_0+2t(1-t)\omega_1+ t^2 \omega_2} \] 其中:

$C_{sf} = $是形状因子，决定了圆锥曲线的类型。当$C_{sf}=1$时，曲线为抛物线。而对于$C_{sf}<1$，曲线为椭圆，当$c_{sf}=0$，曲线退化为一条直线，当$c_{sf}>1$，曲线为双曲线，当$C_{sf} $，曲线退化为两条直线。

NURBS的修改

我们可以通过修改权重，控制点以及节点来修改NURBS曲线。对于权重，如果增加或者减少一个控制点的权重，曲线会向控制点靠近或远离。如果希望一个点$S$朝着控制点$P_i$靠近或原理距离$d$，可以修改权重: \[ \omega^* = \omega_i\left[ 1 + \frac{d}{R_{i,k}(t)(P_iS - d)}\right]. \] 对于控制点的修改，也会改变NURBS曲线的形状。我们还可以通过带约束的优化方法，来求解对于每个控制点的修改量，以得到最佳的修改量（比如需要经过空间中的某个点）。

NURBS曲面的定义也就是曲线简单的拓展： \[ P(u,v) = \frac{\sum_{i=0}^m\sum_{j=0}^n \omega_{ij} P_{ij} N_{i,p}(u)N_{j,q}(v)}{\sum_{i=0}^m\sum_{j=0}^n \omega_{ij} N_{i,p}(u)N_{j,q}(v)} = \sum_{i=0}^m\sum_{j=0}^n P_{ij}R_{i,p;j,q}(u,v) , u,v\in[0,1] \] 上式中： \[ R_{i,p;j,q}(u,v) = \frac{ \omega_{ij} N_{i,p}(u)N_{j,q}(v)}{\sum_{r=0}^m\sum_{s=0}^n \omega_{rs} N_{r,p}(u)N_{s,q}(v)} \] NURBS曲面也具有可微性，同时存在局部极值点，也具有和B样条曲面类似的多种性质。这里就不过多介绍了。