SLAM——视觉里程计(五)光流法和直接法
特征点法是提取特征,根据稀疏特征点的对应点来计算相机的位姿变换。但是它是有比较明显的缺点的:1.特征点的提取比较耗时,限制了SLAM的运行速度,2. 特征点过于稀疏,可能会浪费很多有用信息 3. 我们在生活中总会遇到纹理特征缺失的情况,比如一面白墙,这时候我们找不到足够的特征点来得到相机的运动。所以我们来讨论另外的两种方法,叫做光流法和直接法。
光流法
光流是一种描述像素随时间在图像之间运动的方法,随着时间的流逝,同一个像素会在图像中运动,而我们希望追踪它的运动过程。如果只计算部分像素的运动我们称为稀疏光流,计算所有像素的运动我们称为稠密光流。其中,稀疏光流以Lucas-Kanade光流为代表,可以在SLAM中用于追踪特征点的位置,因此我们主要了解以下LK光流。
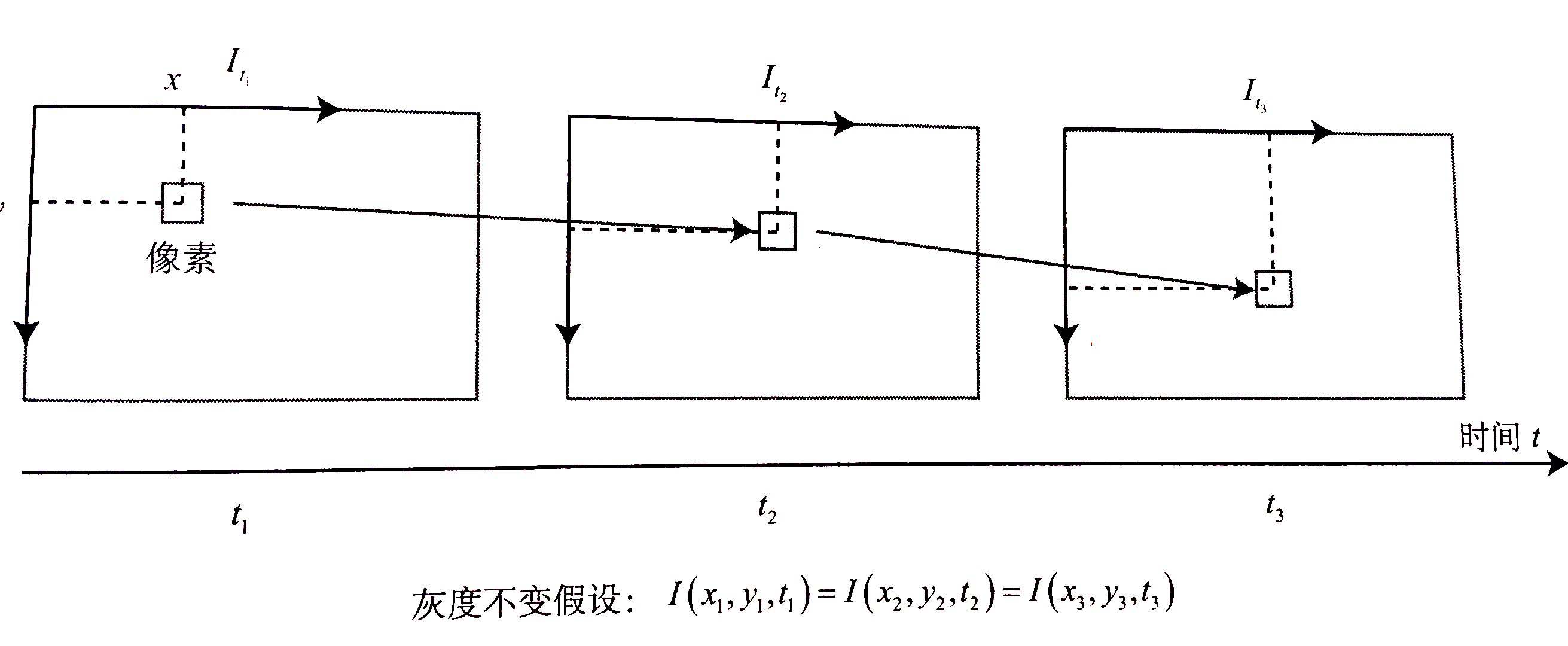
在LK光流中,我们认为来自相机的图像是随着时间变化的,而图像可以看成时间的函数:\(I(t)\)。那么在\(t\)时刻,位于\((x,y)\)的像素它的灰度为:\(I(x,y,t)\)。现在考虑某个固定的空间点,它在t时刻的像素坐标为\((x,y)\)。我们假设在相机运动中,同一个空间点的像素灰度是不变的,这个假设叫灰度不变假设。这个假设是一个强假设,因为实际中灰度一般都会变化。
现在假设在\(t+dt\)的时刻它的位置运动到了\((x+dx,y+dy)\),则我们可以得到: \[ I(x,y,t) = I(x+dx, y+dy,t+dt) \] 如果对上式中右侧进行一介泰勒展开: \[ I(x+dx,y+dy,t+dt) \approx I(x,y,t)+\frac{\partial I}{\partial x}dx + \frac{\partial I}{\partial y}dy + \frac{\partial I}{\partial t}dt \] 由此可以得到: \[ \frac{\partial I}{\partial x}dx + \frac{\partial I}{\partial y}dy + \frac{\partial I}{\partial t}dt = 0. \] 对两侧同时除以\(dt\),我们得到: \[ \frac{\partial I}{\partial x}\frac{dx}{dt} + \frac{\partial I}{\partial y}\frac{dy}{dt} = -\frac{\partial I}{\partial t}. \] 其中\(\frac{dx}{dt},\frac{dy}{dt}\)为像素在\(x,y\)轴上的运动速度,把它们分别记为\(u,v\)。同时\(\frac{\partial I }{\partial x},\frac{\partial I}{\partial y}\)记为图像在\(x,y\)方向上的梯度,分布记为\(I_x,I_y\)。再把图像灰度对于时间的变化量记为\(I_t\),则我们可以把上式写为: \[ \begin{bmatrix} I_x&I_y \end{bmatrix} \begin{bmatrix} u\\ v \end{bmatrix} = - I_t \] 我们想计算的是像素运动\(u,v\),但上面的单个式子是无法计算出来的。因此需要额外的约束,在LK光流中,我们假设某个窗口内的像素具有相同的运动。现在考虑一个大小为\(w\times w\)的窗口,它还有\(w^2\)数量的像素。由于该窗口内像素具有同样的运动,因此方程个数为\(w^2\)个。记: \[ A=\begin{bmatrix} [I_x,I_y]_1\\ \vdots\\ [I_x,I_y]_k \end{bmatrix},b=\begin{bmatrix} I_{t1}\\ \vdots\\ I_{tk} \end{bmatrix} \] 我们得到: \[ A\begin{bmatrix} u\\ v \end{bmatrix} =- b \] 对于这个超定方程,我们可以使用最小二乘解: \[ \begin{bmatrix} u\\ v \end{bmatrix}^* = -(A^TA)^{-1}A^Tb \] 在稀疏光流法中我们依然需要计算特征点,不过可以只计算关键点。通过对特征点的追踪来得到构成方程\(u,v\)。由于像素梯度仅在局部有效,所以如果一次迭代结果不够,我们会多迭代几次这个方程。在SLAM中,LK光流经常被用来追踪角点的运动。
在实践中,对于光流法对于角点的追踪效果最好,对于边缘与区块中的特征点效果较差,可能会追踪失败。
直接法
对于直接法,它和光流法有一样的前提假设,即灰度不变。假如\(p_1,p_2\)分别是空间中同一个坐标点在两个不同位姿的相机下的投影坐标,我们现在想求的是这两个坐标之间的相对位姿,从\(P_1\)到\(P_2\),则: \[ p_1 = \begin{bmatrix} u_1\\ v_1\\ 1 \end{bmatrix} = \frac 1 {Z_1}KP,\\ p_2 = \begin{bmatrix} u_2\\ v_2\\ 1 \end{bmatrix} = \frac 1 {Z_2}K(RP+t) = \frac{1}{Z_2}K(\exp(\xi ^{\hat{} })P) \] 上述坐标依然包含了齐次到非齐次的转换。通过上式,我们知道了\(p_1,p_2\),不过直接法可以不用提取特征点,因此我们并不知道他们在图像上真正的对应关系,只得到了一个预测值。这时候,我们就需要使用灰度不变的假设了,将重投影误差转换成灰度之间的差异,叫做光度误差,也就是两个像素的亮度误差: \[ e = I_1(p_1) - I_2(p_2) \] 当然我们对优化目标依然取二范数。 \[ \xi^* = \arg\min_{\xi} J(\xi) = \sum_{i=1}^n\Vert e \Vert^2 \] 不过现在先关注\(e\)的导数。使用李代数上的扰动模型,则: \[ \begin{aligned} e(\xi \oplus \delta \xi) &= I_1\left(\frac 1 {Z_1}KP\right) -I_2\left(\frac 1 {Z_2} K \exp(\delta \xi ^{\hat{} }) \exp(\xi ^{\hat{} })P\right) \\ &\approx I_1\left(\frac 1 {Z_1} K P\right) - I_2\left(\frac{1}{Z_2}K(1+\delta\xi^{\hat{} })\exp(\xi^{\hat{} })P\right)\\ &=I_1\left(\frac 1 {Z_1}KP\right) - I_2\left(\frac 1 {Z_2} K \exp (\xi^{\hat{} })P + \frac 1 {Z_2}K\delta\xi^{\hat{} }\exp(\xi^{\hat{} })P\right) \end{aligned} \] 记: \[ q = \delta \xi ^{\hat{} } \exp(\xi^{\hat{} })P, u = \frac 1 {Z_2}Kq \] 这里的\(q\)为扰动分量在第二个相机坐标系下的坐标,\(u\)为它的像素坐标。利用一阶泰勒展开,可以得到: \[ \begin{aligned} e(\xi \oplus \delta \xi) &= I_1\left(\frac 1 {Z_1}KP\right) - I_2\left(\frac 1 {Z_2} K \exp(\xi^{\hat{} })P + u \right)\\ &\approx I_1\left(\frac{1}{Z_1}KP\right) - I_2\left(\frac{1}{Z_2}K\exp(\xi^{\hat{} })P \right) - \frac{\partial I_2}{\partial u}\frac{\partial u}{\partial q} \frac{\partial q}{\partial \xi}\delta\xi\\ &= e(\xi) - \frac{\partial I_2}{\partial u}\frac{\partial u}{\partial q} \frac{\partial q}{\partial \xi}\delta\xi \end{aligned} \] 可以看到一阶导数由于链式法则分成了3层。而这3层都是比较容易计算的:
- \(\frac{\partial I_2}{\partial u}\)为\(u\)处的像素梯度
- \(\frac{\partial u}{\partial q}\)为投影方程关于相机坐标系下的三维点的导数。即\(q=[X,Y,Z]^T\),根据上一次PnP下的推导可以得到: \[\frac{\partial u}{\partial q} =\begin{bmatrix} \frac{\partial u}{\partial X}&\frac{\partial u}{\partial Y}&\frac{\partial u}{\partial Z}\\ \frac{\partial v}{\partial X}&\frac{\partial v}{\partial Y}&\frac{\partial v}{\partial Z} \end{bmatrix} = \begin{bmatrix} \frac{f_x}{Z} & 0 & -\frac{f_xX}{Z^2}\\ 0&\frac{f_y}{Z}&-\frac{f_yY}{Z^2} \end{bmatrix}\]
- \(\frac{\partial q}{\partial \xi} = (q)^{\odot}\)
在实践中,由于后两项只和三维点\(q\)有关,与图像无关,因此常常将他们合并: \[ \frac{\partial u}{\partial \xi} = \begin{bmatrix} \frac{f_x}{Z'} & 0 & -\frac{f_xX'}{Z'^2} & -\frac{f_xX'Y'}{Z'^2} & f_x + \frac{f_xX^2}{Z'^2} & -\frac{f_xY'}{Z'}\\ 0 & \frac{f_y}{Z'} & -\frac{f_yY'}{Z'^2} &-f_y - \frac{f_yY'}{Z'^2} & \frac{f_yX'Y'}{Z'^2} & \frac{f_yX'}{Z'} \end{bmatrix} \] 这个矩阵在之前的pnp中也出现过。因此: \[ J =\lim_{\delta\xi \rightarrow 0}\frac{e(\xi \oplus \delta \xi)-e(\xi) }{\delta \xi}= -\frac{\partial I_2}{\partial u}\frac{\partial u}{\partial \xi} \] 这就是直接法的雅科比矩阵。
不过直接法有明显的优点,但也有明显的缺点。由于图像的非凸性,直接法往往找到的是极小值。单个像素没有区分度,因此我们计算的是像素块。最重要的是灰度不变是很强的假设,这意味着直接法只有在特定的条件下才能有比较好的效果。