信息论——信道及其容量（二）

到目前为止，我们都只算出来了信道容量，没有讲过怎么编码能得到这些容量。接下来要做的就是说明，所有上面算出来的容量，都是可以实现的。

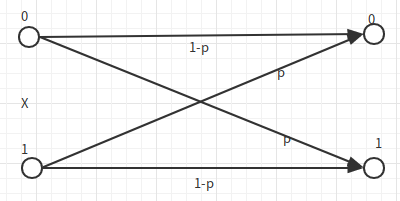
一个信道如下图：

信道编码

这里我们先回忆一下之前的混乱打字机。之前说过，世界上任何一个数字信道，都可以直接或者间接地看作是混乱打字机模型。

对于信道\(\{X,q(y|x),Y\}\)的信道编码包含以下要素：

• 输入符号集合\(\{1,2,…,M\}\)
• 编码函数\(X^n\):\(\{1,2,…,M\} \rightarrow X^n\)，该函数为每一个输入符号产生了相应的信道编码码字\(X^n(1),X^n(2),…,X^n(M)\)，这些码字构成的集合称为“码本”。
• 解码函数\(g\):\(Y^n \rightarrow \{1,2,…,M\}\)，该函数为一个确定性判决函数，将每一个可能的接受向量映射到一个输入符号。

意思也就是，对于符号个数为\(M\)的符号集，我们把它映射到一个长度为n的序列上,分n次传输。

信道编码的码率

\((M,n)\)码的码率Ｒ定义为： \[ R = \frac{\log M}{n} , \] 单位为比特/传输。这是信道码的每个码字母所能携带的最大的信息量。

如何理解？对于输入集合如果取等概分布，则它的信息量为\(\log M\)，这时候呢，\(n\)次传输才能传达这么多的信息量，所以每个传输的量就是\(\frac{\log M}{n} = R\)，则\(M = 2^{nR}\)。称这样的码为\((2^{nR},n)\)码。

Example

重复码，输入字母数\(M = 2\):\(\{0,1\}\)，重复n次，这个码率为\(1/n\)。

直观来说，如果字符个数为\(M\)个，我们需要编码长度为\(log M\)就够了，这时候就可以保证码率为1。那为什么要进行这么复杂的定义？因为我们需要知道信道的传输是有噪声的。因此往往码率是要小于1，也就是n个长度本可以表示更大的字符集，但是我们选择它，增加码的冗余度，来降低错误率。比如下面的例子。

二进制奇偶校验码，输入字母数\(M = 2^{n-1}:{x_1,x_2,…,x_{n-1} }\)，信道编码方案为\(C = x_1,x_2,…,x_{n-1}x_{\text{parity} }\)，其中\(x_{\text{parity} }\)用于辨识码字中\(1\)的个数为奇数还是偶数，这个码率为：\(\frac{n-1}{n}\)。

信道编码的错误概率

输入为符号\(i\)时的条件错误概率为： \[ \begin{aligned} \lambda_i &= Pr\{g(Y^n) \ne i \vert X^n = x^n(i)\}\\ &= \sum_{y^n} q(y^n\vert x^n(i))I(g(y^n) \ne i) \end{aligned} \] 其中\(I(\cdot)\)为指示函数。

\((M,n)\)码的最大错误概率为： \[ \lambda^{(n)} = \max_{i \in 1,2,...M} \lambda_i \] \((M,n)\)码的算术平均错误概率为： \[ P_e^{(n)} = \frac{1}{M} \sum_{i=1}^M\lambda_i \] 我们称一个码率\(R\)是可达的，若存在一个信道编码\((\lceil 2^{nR}\rceil,n )\)，其最大差错概率在\(n\rightarrow \infty\)时趋于0。可以看出来可达要求无差错，而且是渐进的。

这时候我们得到信道容量的另外一个定义：一个信道的容量是该信道上所有可达码率的上确界，即\(C = \text{sup }R\)，这意味着\(C\)一定对应着一种信道编码方案。

经验主义式的设计

在信道传输中如何减少差错？由香农公式： \[ C_T(\beta) = WT \log(1+\frac{P_S}{N_0W}) \] 可以得到，提高抗干扰能力的方法如下：

1. 增加功率(提高信噪比)
2. 加大带宽(信号变化剧烈)
3. 延长时间(降低速率)

\(C = max_{p(x),功率约束}\{I(X;Y)\}\)

而降低重复速率，实际上就是重复，增加冗余。

重复码

最直观的纠错方法就是：重复，增加冗余。

• 编码１：将每个输入元重复三次
  • 纠正任一位上的错误
  • 设码字记为\((c_8,c_7,…,c_0)\)
  • 由编码方法可知，信道无误时：\[ c_8 = c_7 = c_6\\ c_5 = c_4 = c_3\\ c_2 = c_1 = c_0\]
  • 解码时，若\(c_8 = c_6 \ne c_7\)，则判定\(c_7\)位出错，采用简单多数法进行判定
  • 依据是：连续出现两个错误的概率远远小于出现一个错误的概率

如下图，如果我们将上述编码放进二进制对称信道，则想要得到无差错编码。误码率的大小是重复\(2n+1\)次，而至少出现了\(n+1\)次错误。为了让误码率取0,\(n \rightarrow 0\)，此时码率也趋近于0，这不是一个好消息。

但是，是否对于信息的无差错传输，就意味着码率为0呢？答案是否定的。

现在我们考虑BSC信道，\(W= \{1,2,…,2^k\}\),如下： \[ W=\{1,2,...,2^k\} \rightarrow \text{Encoder} \rightarrow X^n \rightarrow\text{BSC(p)} \rightarrow Y^n \rightarrow \text{Decoder} \rightarrow W \] 我们可以得到： \[ \begin{aligned} nC &\ge nI(X;Y)\\ &\ge I(X^n;Y^n)\\ &\ge I(W,\hat W)\\ &=H(W) - H(W\vert \hat W)\\ &\ge k - k H(P_e) \end{aligned} \] 上式中最后一步是由Fano不等式得到的（不知道怎么得到，实际上我只能得到的是：\(\ge k - (H(P_e)+kP_e)\)）。

则：\[k \leq \frac{nC}{1 - H(P_e)}\]

而由于BSC信道的容量可以得到：\(C = 1 - H(P)\)，所以我们得到一个R的上界： \[ R = \frac{k}{n} \ge \frac{1 - H(P)}{1 - H(P_e)} \] 通过变形，我们可以得到： \[ H(P_e) \ge 1 - \frac C R \rightarrow P_e \ge H^{-1}\left(1 - \frac C R\right) \] 这意味着，如果想要让\(P_e\leq 0\)，则\(R \leq C\)，如果\(R > C\)，则\(H(P_e)>0\)，所以我们一定可以得到\(P_e>0\)，不可能进行可靠通信。

那么无差错传输的情况下，码率最大能有多少？先给你看一个preview，很直白的内容，不过它被证明确实是正确的：

想象信道将信源映射到一个球体里，而对每个输入符号也对应一个球。而这个球的体积就意味着噪声带来的体积，而大球中能容纳多少小球，正是这个信道编码在无错的情况下可以映射的符号数M。因为这个球的维度是n维的，我们可以得到： \[ M = \frac{\left[\sqrt{P_S +P_N}\right]^n}{\left[\sqrt{P_N}\right]^n} = (1 + \frac{P_S}{P_N})^{\frac n 2} \] 由上式，可以计算得出： \[ R = \frac 1 2 \log (1 + \frac{P_S}{P_N}) \] 而这个值，正好与连续无记忆加性高斯噪声信道的容量一致。

当然，这个只是preview，不是严格的证明过程。下面对这个证明进行稍微严谨地推导，说明大多数噪声信道都有这样地特性。

为了证明这个东西，我们需要介绍一些别的定义。之前证明信源无失真压缩定理地时候，用到了典型序列，而这次我们在典型序列地基础上，重新介绍一个新的内容。

证明香农第二定理

联合典型序列

设\((X^n,Y^n)\)是长为\(n\)的随机序列对，其概率分布满足

p(x^n,yn) = _{i=1}^n p(x_i,y_i)

若\((X^n,Y^n)\)满足以下条件，则称其为联合典型序列：

• \(\lvert -\frac 1 n \log p(x^n) - H(X) \rvert < \epsilon\)
• \(\lvert -\frac 1 n \log p(y^n) - H(Y) \rvert < \epsilon\)
• \(\lvert -\frac 1 n \log p(x^n,y^n) - H(X,Y)\rvert < \epsilon\)
  联合典型序列构成的集合为\(A_\epsilon^{(n)}\)。

联合典型序列与之前典型序列定义是有很大地相似性：信息论——Lossless-Encoding。我们首先要看看联合典型序列的性质，才能用它来证明。

联合渐进等同分割定理（Joint AEP）

设\((X^n,Y^n)\)是长度为\(n\)的随机序列对，其分布满足： \[ p(x^n,y^n) = \prod_{i=1}^n p(x_i,y_i) \] 则以下性质成立：

• 当\(n \rightarrow \infty\)时，\(Pr((X^n,Y^n) \in A_\epsilon ^{(n)}) \rightarrow 1\)
• \((1 - \epsilon)2^{n(H(X,Y) - \epsilon)} \leq \vert A_\epsilon ^{(n)} \vert\leq 2^{n(H(X,Y)+\epsilon)}\)
• 设$(,)p(x^n)p(yn) \(,即\),\(统计独立，且具有与\)p(x^n,yn)$一致的边缘分布，则： \[Pr\left((\tilde{X^n},\tilde{Y^n}) \in A_\epsilon ^{(n)}\right) \leq 2^{-n(I(X;Y) - 3\epsilon)}\] 若\(n\)足够大，则： \[Pr\left((\tilde{X^n},\tilde{Y^n}) \in A_\epsilon ^{(n)}\right) \ge (1 - \epsilon)2^{-n(I(X;Y) + 3\epsilon)}\]

前两点都比较好理解，第三点中，\((\tilde{X^n},\tilde{Y^n})\)是由\((X^n,Y^n)\)的边缘分布依照\(X^n,Y^n\)独立形成的另一个联合分布，而这个分布属于典型序列的概率约等于\(2^{-nI(X;Y)}\)。

在这里我们证明以下第三条的前半部分： \[ \tilde{X^n},\tilde{Y^n}\text{ are independent. }\tilde{X^n}\sim P_X(x^n),\tilde{Y^n}\sim P_Y(y^n)\\ \begin{aligned} Pr\{(\tilde{X^n},\tilde{Y^n}) \in A_\epsilon^{(n)} \} &= \sum_{(\tilde{x^n},\tilde{y^n}) \in A_\epsilon^{(n)} } P(x^n)P(y^n)\\ &\leq 2^{b(H(X,Y) + \epsilon)}\cdot 2^{-n(H(X) - \epsilon)} \cdot 2^{-n(H(Y) - \epsilon)}\\ &= 2^{-n(I(X;Y) - 3\epsilon)} \end{aligned} \] 下图可以帮助我们更好地理解这些性质：

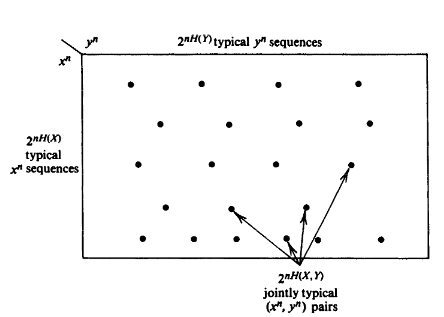
• 联合分布中，大约有\(2^{nH(X)}\)个典型X序列和\(2^{nH(Y)}\)个典型Y序列
• 其组合共有\(2^{nH(X) + nH(Y)}\)个，但是其中联合典型的只有\(2^{nH(X,Y)}\)个
• 随机选择而出现联合典型序列的概率为\(2^{-nI(X;Y)}\)

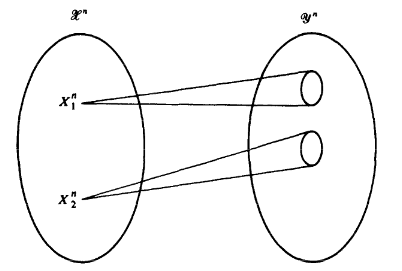
现在来看一下联合典型序列的另一个解释：

• 对于典型输入序列\(x^n\)，存在大约\(2^{nH(Y|X)}\)个可能的输出，且它们等概
• 所有可能的典型输出序列大约有\(2^{nH(Y)}\)个，这些序列被分成若干个不相交的子集
• 子集个数为\(2^{n(H(Y) - H(Y|X))} = 2^{nI(X;Y)}\)，表示信道可以无错误传递的最大字母序列个数

对于定理的证明包含两部分，一是可达性，也就是这个容量是可达的，第二个就是证明不可能达到比这个容量更好的速率。

可达性的证明

可达性的证明也就是我们可以找到一个编码函数和解码函数，使得信道带到容量C，而且是无差错地传输。 \[ W \in [1:2^{nR}] \rightarrow X^n \sim P_X(x) \rightarrow q(y|X)\rightarrow Y^n\rightarrow \hat W \] 很反直觉的是，香农给我们编码方法是随机编码。这个随机编码指的是生成码字的过程为随机的： \[ \text{Random Code:}\\ \ell =\begin{pmatrix} x^n(1)\\ x^n(2)\\ \vdots\\ x^n(2^{nR}) \end{pmatrix} \] 其中\(x^n(k)\)是独立同分布的生成的，分布为\(P_X(x^n(k)) = \prod_{i=1}^n P_X(x_i(k))\)

于是我们得到了码本，信源发送\(x^n(k)\)，而解码器收到\(y^n\)，一个长度为n的序列。

解码过程：如果解码器端找到唯一的\((x^n(\hat k), y^n) \in A_{\epsilon}^{(n)}\)，则解码得到\(\hat k\)。也就是\(y^n\)和一个唯一的\(\hat k\)对应的编码序列\(x^n(\hat k)\)属于联合典型序列，则解码为\(\hat k\)，否则解码出错。

现在我们分析一下出错概率。假设1为被传输的符号，而\(y^n\)为对应的输出。那么\(x^n(1)\)与\(y^n\)为联合典型序列的概率非常高。而另外一个i对应的\(x^n(i)\)与\(y^n\)为联合典型序列的概率就没有那么高了。实际上这个概率和联合典型序列性质的第三条是一致的。\(x^n(i),y^n\)有很大的概率是边缘典型序列，而随意两个边缘典型序列组合为联合典型序列的概率，正是 \[ Pr\left((\tilde{X^n},\tilde{Y^n}) \in A_\epsilon ^{(n)}\right) \approx 2^{-nI(X;Y)}. \] 出错的类型有两种。

1. 传的是1,而没有联合典型，
2. 传的是1,有多个和它是联合典型。 \[ \begin{aligned} P(E) &= P(E_1\cup E_2)\\ &\leq P(E_1)+P(E_2)\\ &\leq \epsilon + \sum_{i=2}^{2nR}2^{-n(I(X;Y) - 3\epsilon)}\\ &\leq \epsilon + 2^{3n\epsilon}2^{-n(I(X;Y) - R)} \end{aligned} \] 我们希望\(P(E) \rightarrow 0\)，而第一项是可以任意小的，我们真正在意的是想要\(I(X;Y)-R >0\)。如果我们把生出随机码本的\(P_X(x)\)固定到\(P^*_X(x)\)，则\(I(X;Y) = C\)，于是只要\(R<C\)即可。

这个证明并不严谨，但是给我们提供了一个很重要的思维脉络。我们证明了\(R < C\)的情况下，可以实现无差错传输。

下面要说明的是定理的逆的证明。

converse证明

\[ \begin{aligned} nR &= H(W)\\ &= H(W|\hat W) + I(W;\hat W)\\ &= I(W;\hat W)\\ &\leq I(X^n(W);Y^n)\\ &= H(Y^n) - H(Y^n|X^n)\\ &\leq \sum_{i} H(Y_i) - \sum_{i}H(Y_i|X_i)\\ &= \sum_{i} I(X_i;Y_i)\\ &\leq nC \end{aligned} \] 由此我们证明了，要想实现无差错的传输，那么\(R\leq C\)是一定成立的。由此香农第二定理的证明就结束了。和无差错编码一样，随机编码在现实中由于码本巨大也是难以实现的。不过在信息论提出的60年中，人类一次次提出新的编码，像香农界不断逼近。看着这些进步，感觉自己的信息论虽然没什么用到过，但是也没有白学。