Learning From Data——Kernel PCA
上次说了几个PCA的局限性,其中有一个是它只找各个特征之间的线性关系。如何拓展线性关系到非线性,似乎有点思路,因为之前SVM中说过,可以通过kernel将SVM拓展到非线性的分类。同样通过kernel,我们也可以找到特征之间的非线性关系,从而利用PCA进行数据压缩等操作。
对于线性的PCA的扩展,就是将PCA映射到更高维度的空间,使其在更高维度的空间有线性关系:\(\phi:\mathbb{R}^n \rightarrow \mathbb{R}^d,d\ge n\).而如何映射,通过一个kernel函数来定义:\(k(X_i,X_j) = \phi(X_i)^T\phi(X_j)\)或者kernel矩阵\(K \in \mathbb{R}^{m \times m}\). 映射完成后,我们就可以在更高维度的空间再使用标准的PCA算法了。不过这个想法是naive的,比如高斯核函数,是映射到无限维度,如果用原来的PCA去求,是不现实的。而且,从下面的分析可以看到,直接求也用不到kernel函数的方便之处。
映射后的数据的协方差矩阵如下: \[ \Sigma = \frac 1 m \sum_{i=1}^m \phi(X_i) \phi(X_i)^T \in \mathbb{R}^{d\times d} \]
假如\((\lambda_k,v_k),k=1,...,d\)为\(\sigma\)的特征分解,则: \[ \Sigma v_k = \lambda_k v_k \]
则原来\(X_l\)的在第k个主要成分的投影为:\(\phi(X_l)^Tv_k\).
到目前位置,我们都没有用到kernel。\(\phi(X_i)\)是难以计算的,而kernel是容易计算的。因此如何避免\(\phi_(X_i)\)的计算?
首先我们知道: \[ \begin{align} \Sigma v_k = \left (\sum_{i=1}^m \phi(X_i) \phi(X_i)^T \right ) v_k = \lambda _k v_k \end{align} \]
实际上,我们可以将\(v_k\)写成\(\phi(X_i)^T\)的组合(这个很像是之前的kernel logistic regression用的trick),这里就不证明为什么一定可以写成这个组合了,我觉得应该会用到线性代数的秩的知识。 \[ v_k = \sum_{i = 1} ^m \alpha_i^{(k)} \phi(X_i) \]
那么,之前提到的投影可以将上式带入: \[ \begin{aligned} \phi(X_l)^Tv_k &= \phi(X_l)^T \sum_{i = 1} ^m \alpha_i^{(k)} \phi(X_i)\\ &= \sum_{i=1} ^m \alpha_i^{(k)} \phi(X_l)^T\phi(X_i)\\ &= \sum_{i=1} ^m \alpha_i^{(k)} k(X_l,X_i) \end{aligned} \]
这又引入了一个问题:如何得到\(\alpha_i^{(k)}\)?
将\(v_k = \sum_{i = 1} ^m \alpha_i^{(k)} \phi(X_i)\)带入(1)式,我们得到: \[ \left[\sum_{i=1}^m \phi(X_i) \phi(X_i)^T \right] \left(\sum_{i=1}^m \alpha_i^{(k)} \phi(X_i) \right) = \lambda_k m \left(\sum_{i=1}^m \alpha_i^{(k)} \phi(X_i) \right)\\ \Phi(X)^T \Phi(X) \Phi(X)^T \alpha^{(k)} = \lambda_k m \Phi(X)^T \alpha^{(k)}\\ \Phi(X) \Phi(X)^T \alpha^{(k)} = \lambda_k m \alpha^{(k)}\\ K \alpha^{(k)} = \lambda_k m \alpha_k, \] 上式中: \[ \alpha ^{(k)} = \begin{bmatrix} a_1^{(k)}\\ \vdots\\ a_m^{(k)} \end{bmatrix};\Phi(X) = \begin{bmatrix} \phi(X_1)^T\\ \vdots\\ \phi(X_m)^T \end{bmatrix} \\ K = \begin{bmatrix} k(X_1,X_1)&k(X_1,X_2)&\cdots&k(X_1,X_m)\\ k(X_2,X_1)&k(X_2,X_2)&\cdots&k(X_2,X_m)\\ \vdots&\vdots\ &\ddots&\vdots\\ k(X_m,X_1)&k(X_m,X_2)&\cdots&k(X_m,X_m) \end{bmatrix} \]
上式中\(\alpha^{(k)}\)可以通过求解K的特征向量得到,而K是kernel矩阵。
我们希望正交化\(\alpha^{(k)}\),使得\(v_k^Tv_k = 1\)(与之前的标准PCA一致). \[ v_k^T v_k = (\alpha^{(k)})^T \Phi(X) \Phi(X)^T \alpha^{(k)} = \lambda_k m ((\alpha^{(k)})^T \alpha^{(k)}). \]
所以$^{(k)} ^2 = $.
此外,如果\(\mathbb{E}(\phi(X)) \ne 0\),我们还需要中心化\(\phi(X)\): \[ \tilde{\phi}(X_i) = \phi(X_i) - \frac 1 m \sum_{l=1}^m \phi(X_i) \]
而中心化以后的kernel矩阵为: \[ \tilde{k}(i,j) = \tilde{\phi}(X_i)^T \tilde{\phi}(X_j) \]
写成矩阵就是: \[ \tilde{K} = K -1_m K - K 1_m + 1_mK1_m \]
其中: \[ 1_m = \begin{bmatrix} \frac 1 m & \cdots &\frac 1 m\\ \vdots & \ddots & \vdots\\ \frac 1 m & \cdots &\frac 1 m \end{bmatrix} \in \mathbb{R}^{m\times m} \]
我们从前面已经推导出来,计算kernel PCA的\(v_k\)最终需要的是kernel矩阵,因此使用\(\tilde{K}\)去计算PCA即可。
2个问题:
- 之前的X不光是中心化的,而且还是Stdev(X) = 1,在kernel PCA中没有考虑这一点吗?
对于kernel PCA的标准协方差分析是非常困难的。不过协方差的意义在于使得数据范围不会变动过大(如身高m为单位,变化程度可能是1以内,而体重以斤为单位,变化范围为几十),因此如果对原数据进行协方差变0的操作后,假设kernel是对称的,它们的变化范围不会差得过多。
- \(a^{(k)}\)算出来有m个,但是我们不一定把它映射到m维度的空间了。不像原来的PCA,n维有n个特征向量?
一般来说我们升维时候都会升到无限维度,很少有比m小的。这时候它的特征向量个数就受到了数据个数的限制。如果维度比m小,则特征向量不会真正达到m个。
总结以下,kernel PCA的步骤:
求出K
求出\(\tilde{K}\)
求出上面的特征值和特征向量,并且根据使得特征向量的长度等于\(\frac {1}{\sqrt{\lambda_k m} }\),其中\(\lambda_km\)也就是对应的特征值。
根据求得的特征向量,求得\(v_k\).
Kernel PCA的例子: 
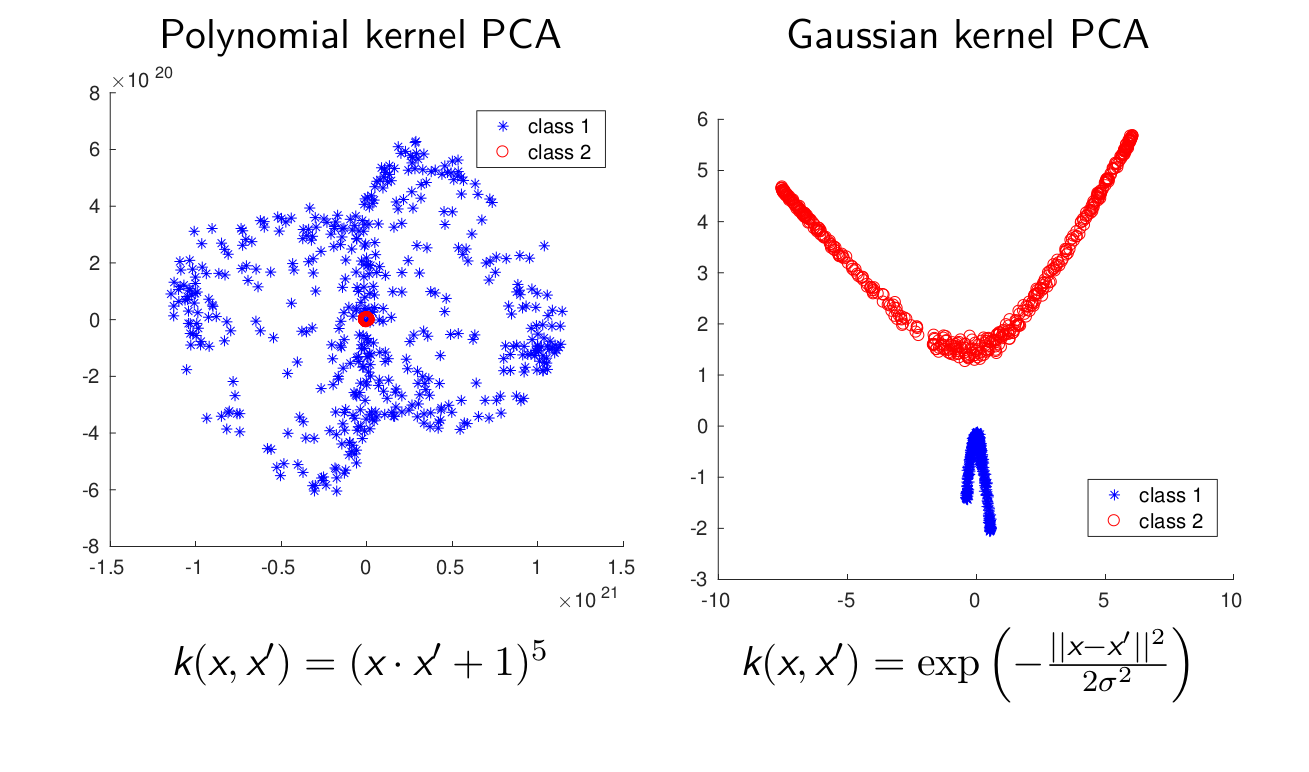
kernel PCA经常用于聚类,异常检测等等。它需要找到\(m \times m\)的特征向量来代替\(n \times n\)。通过投影到k维主子空间进行降维通常是不可能的,也就是一般不用kernel PCA来进行数据压缩。