Learning From Data——Neural Network
这周上的数据学习,主要讲了一些神经网络相关的知识。神经网络是目前最流行的机器学习算法了,甚至由它诞生了一个新的学科:deep learning。因此一篇博客,只能浅浅介绍一些神经网络的基本内容。 据说神经网络制造出来是为了模拟大脑。不过我认为离这个目标还差的远。但是呢,Neural Network确实做出来一些很牛逼的事情,让它成为现在AI中最受欢迎的技术。不过神经网络的概念倒是很早很早就提出了,之前没落是因为计算的性能跟不上。现在又东山再起了。
即使没有接触过机器学习,也一定听过神经网络学习,以及见过类似下面的图:
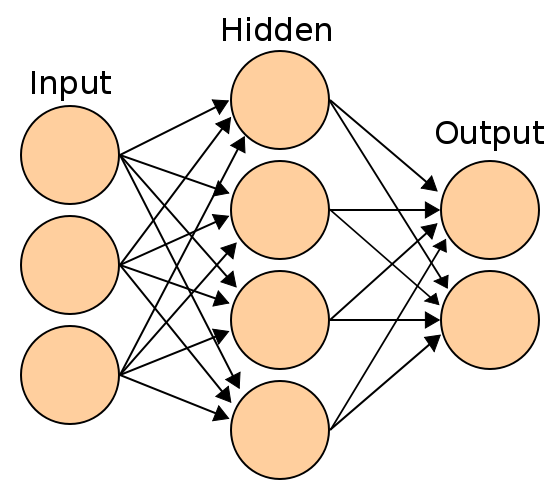
实际上,这就是神经网络。神经网络的原理不复杂,但是如果嵌套层数比较多,就会需要非常大的计算量。
对于每一个神经元,我们都可以把它看作之前的一个logistic regression。每一个神经元可以接受输入,然后提供输出,要么作为最终的输出,要么给别的神经元提供输入。
前向传播(forward propagation)
这意味着,我们的\(W\)参数将会变成一个”张量”(这么说也许不够准确,因为它不第一层可能有5个神经元,第2层可能有4个,也就是不是一个立方体)。在这里,我们用\(\Theta\)来表示这个张量。\(\Theta^{(i)}\)表示第i层的\(\theta\)参数,而\(\Theta^{(i)}_j\)表示第i层,第j个theta向量,\(Theta^{(i)}_{j,k}\)表示的就是某个具体的参数值了。
我们使用\(a^{(i)}_j\)按照上面的规则来表示第i层第j个神经元的输出。
所以,就上面的这个图,我们可以很容易得出: \[ a_1^{(1)} = g(\Theta_{1,0}^{(1)}x_0 + \Theta_{1,1}^{(1)}x_1 + \Theta_{1,2}^{(2)}x_2+\Theta_{1,3}^{(3)}x_3 )\\ a_2^{(1)} = g(\Theta_{2,0}^{(1)}x_0 + \Theta_{2,1}^{(1)}x_1 + \Theta_{2,2}^{(2)}x_2+\Theta_{2,3}^{(3)}x_3 )\\ a_3^{(1)} = g(\Theta_{3,0}^{(1)}x_0 + \Theta_{3,1}^{(1)}x_1 + \Theta_{3,2}^{(2)}x_2+\Theta_{3,3}^{(3)}x_3 ) a_4^{(1)} = g(\Theta_{4,0}^{(1)}x_0 + \Theta_{4,1}^{(1)}x_1 + \Theta_{4,2}^{(2)}x_2+\Theta_{4,3}^{(3)}x_3 )\\ h_{\Theta}(X) =\\ \begin{bmatrix} g(\Theta_{1,0}^{(2)}a_0^{(1)} + \Theta_{1,1}^{(2)}a_1^{(1)} + \Theta_{1,2}^{(2)}a_2^{(1)} +\Theta_{1,3}^{(2)}a_3^{(1)}+\Theta_{1,4}^{(2)}a_4^{(1)} )\\ g(\Theta_{2,0}^{(2)}a_0^{(1)} + \Theta_{2,1}^{(2)}a_1^{(1)} + \Theta_{2,2}^{(2)}a_2^{(1)} +\Theta_{2,3}^{(2)}a_3^{(1)}+\Theta_{2,4}^{(2)}a_4^{(1)} ) \end{bmatrix}\\ = [a_1^{(2)},a_2^{(2)} ]^T \]
上面的神经网络输出有两项。
上面的函数中,g为logistic函数,又叫sigmoid函数。当然这个函数不仅仅局限于sigmoid函数,也有relu函数,tanh函数: \[ \begin{matrix} g(z) = \frac 1 {1+e^{-z} } &(sigmoid)\\ g(z) = \max(z,0) &(ReLU)\\ g(z) = \frac{e^z - e^{-z} }{e^z + e^{-z} }& (tanh) \end{matrix} \]
我们定义\(a_{j}^1\)为原始输入。
我们可以使用向量化来加速神经网络的计算过程。这个应该不算很稀奇的技术。对于每一层来说,\(theta\)都是严格的矩阵的,而输入也是一个矩阵。所以每一层的向量化都不算困难。
通过输入,计算出每一层的输出,然后将这层输出当作下一层的输入,最后得到最后的结果,这就是前向传播。前向传播实际上就是神经网络怎么计算出结果的过程。
利用神经网络我们可以很容易地实现很复杂的非线性函数的边界,从而进行分类。吴恩达在视频中介绍了用神经网络对与,或非以及异或的实现。不过这些都是相对简单的,复杂的神经网络分析其来完全没有这么容易,这也是神经网络强大的一个原因。
为了实现多个分类,我们可以将最后的输出定位k个,分别来判断是否为当前类。这个做法实际上one-Vs-all的做法。
cost function
接下来我们来谈谈neural network的cost function。之前的logistic regression的cost function是通过计算极大似然估计得到的。而神经网络的cost funtion实际上呢也是一样的,不过它的h(x)不再是之前那么简单了,这里的\(W\)变成了\(\Theta\)。而且由于输出可能是多元的(多元分类),所以这个cost funtion实际上是各个类别的cost funtion的叠加: \[ J(\Theta) = -\frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K y_i^{(k)} \log(h_{\Theta}(X_i))_k + (1-y_i^{(k)}) \log (1 - (h_\Theta(X_i))_k) \]
如果加上正则化的话,则正则化项为:\(\frac \lambda {2m} \sum_{l=1}^{L}\sum_{i=1}^{s_{l} }\sum_{j=1}{s_{l-1} } (\Theta_{i,j}^{(l)})^2\)
需要注意的是这个\(s_{l+1}\),为何是这样?\(s_l\)表示了第l层有多少神经元(如果l=0则表示有多少个原始输入),也就表示了有多少个输入向量,而输入向量的长度则由前一个输入的个数决定,因此\(s_{l-1}\)实际上输入向量的长度。所以呢,我们先从层数开始,然后到该层的每个神经元,最后再到每个参数的每个取值。 (这里和吴恩达的课程的表述稍微有点区别,也就是我的输入是表示为第0层,也就是一共有L+1层,而吴恩达的课程中,共有L层,原来的0变成现在的第1层。不过这意味着,从1开始计数,由于第一层是没有theta参数的,所以第一层计算的实际是下一层的theta,而\(s_l\)是下一层的输入向量长度,而\(s_{l+1}\)才是输入向量的个数,至于最后一层的theta由于已经在前一次计算过了,所以这里的regularization为\(\frac \lambda {2m} \sum_{l=1}^{L-1}\sum_{i=1}^{s_{l} }\sum_{j=1}{s_{l+1} } (\Theta_{j,i}^{(l)})^2\)).
向量化(vectorize)
首先,为了方便后面的说明,我们定义
\(z_{j}^{(i)} = (\Theta_{j}^{(i)})^Ta^{(i-1)}\).
而\(a_{j}^{(i)} = g(z_{j}^{(i)})\).
\(a^{(i-1)} = [a_0^{(i-1)},a_1^{(i-1)},...,a_{s_{i-1} }^{(i-1)} ]\)
希望大家还没有忘记这些符号以及下标的意义。
如果一个符号,只有层数的上标,没有下标,则意味着它是一个向量(etc.\(a^{(i)},z^{(i)}\)),或是一个矩阵\(\Theta^{(i)}\).
通过向量化,我们可以像下面一样通过线性代数库的并行优化,很快的计算出来\(z^{(i)}\):
\[ z^{(i)} = \Theta^{(i)} a^{(i-1)} \]
上式中: \[ \Theta^{(i)} = \begin{bmatrix} ... (\Theta_{1}^{(i)})^T ... \\ ... (\Theta_{2}^{(i)})^T ... \\ ...\\ ... (\Theta_{s_i}^{(i)})^T ... \end{bmatrix} \]
从这里,我们也可以知道了,为什么g不用identify function(g(z) = z).因为神经网络的提出,是为了进行非线性的分类和预测。而: \[ \begin{aligned} z^{(i)} &= \Theta^{(i)} a^{(i-1)}\\ &=\Theta^{(i)} g(z^{(i-1)})\\ &=\Theta^{(i)} z^{(i-1)}\\ &= \Theta^{(i)} \Theta ^{(i-1)} z^{(i-2)}\\ &= \Theta^{(i)} \Theta^{(i-1)}...\Theta^{(1)} X_1 \end{aligned} \]
这意味着我们通过线性的函数来做神经网络是无法得到非线性的分类结果的。
如果我们再对训练样本利用向量化, \[ Z^{(l)} = \Theta^{(l)} ( A^{(l-1)})^T \] 这时候呢,Z变成矩阵了(\(s_{l} \times m)\)),A也变成矩阵了($ m s_{l-1} $)。而Z^{(l)}实际如下:
\[ Z^{(l)} =\begin{bmatrix} \vert & ... & \vert\\ z^{(l)[1 ]} & ... &z^{(l)[m ]}\\ \vert & ... & \vert \end{bmatrix} \]
后向传播(back propagation)
参数初始化(Parameter Initialization)
需要注意的是,神经网络中我们不能简单地将参数初始化为0.经过计算你就会明白,如果参数初始化为0,则计算出来的梯度就是一样的,无法进行梯度下降,无论怎么运行,最后得到的结果为\(0.5\)(sigmoid)。可以进行随机初始化,给每个参数一个很小的值\(N(0,0.1)\).
在实际中,证明了有比随机初始化更好的方法来进行初始化:Xavier/He initialization.
\[ \Theta ^{(l)} \tilde{} N\left(0,\sqrt{\frac {2}{s_l + s_{l-1} } } \right) \]
梯度(gradient)
后向传播实际上是建立在梯度下降的基础上的,所以最复杂的部分就是计算梯度了。
假设,这个层数一共有L层,最后的输出是\(a^{L}\),因此cost funtion和L层的参数是直接相关的。所以首先计算的就是cost funtion对\(\Theta^{(L)}\)的梯度。
\[ \begin{aligned} \frac{\partial L(\Theta)}{ \partial \Theta^{(L)} } &= -\frac{\partial}{\partial \Theta^{(L)} } \left((1-y)\log (1 - y') + y\log y'\right)\\ &=-(1 - y)\frac{\partial}{\partial \Theta^{(L)} } \log (1 - g(\Theta^{(L)}a^{(L-1)})) - y \frac{\partial}{\partial \Theta^{(L)} } \log g(\Theta^{(L)}a^{(L-1)})\\ &= (1-y)\frac{1}{1 - g(\Theta^{(L)}a^{(L-1)})} g'(\Theta^{(L)}a^{(L-1)}))(a^{(L-1)})^T - y \frac {1}{g(\Theta^{(L)}a^{(L-1)} } g'(\Theta^{(L)}a^{(L-1)}(a^{(L-1)})^T\\ &= (1-y)\sigma(\Theta^{(L)}a^{(L-1)})(a^{(L-1)})^T - y(1 - \sigma(\Theta^{(L)}a^{(L-1)})) (a^{(L-1)})^T\\ &= (1 - y)a^{(L)} (a^{(L-1)})^T - y (1 - a^{(L)})(a^{(L-1)})^T\\ &= (a^{(L)} - y)(a^{(L-1)})^T \end{aligned} \]
上述推导过程中,g为sigmoid函数,因此\(g' = \sigma' = \sigma(1 - \sigma)\).
\(a^{(i)}\)我们都是可以通过前向传播得到的。
然后我们想要计算的是\(\Theta{(L-1)},...,\Theta{(1)}\)这些的梯度。但是它们是和\(L(\Theta)\)是没有直接的关系的。不过,在微积分中是有链式求导法则的:
\[ \begin{aligned} \frac{\partial L}{\partial \Theta^{(L-1)} } &= \frac{\partial L}{a^{(L)} } \frac{a^{(L)} }{\partial \Theta^{(L-1)} }\\ &=\frac{\partial L}{a^{(L)} } \frac{a^{(L)} }{z^{(L)} } \frac{z^{(L)} }{\Theta^{(L-1)} }\\ &=\frac{\partial L}{a^{(L)} } \frac{a^{(L)} }{z^{(L)} } \frac{z^{(L)} }{a^{(L-1)} }\frac{a^{(L-1)} }{\Theta^{(L-1)} }\\ &=\underbrace{\frac{\partial L}{a^{(L)} } \frac{a^{(L)} }{z^{(L)} } }_{a^{(L)} - y}\underbrace{ \frac{z^{(L)} }{a^{(L-1)} } }_{\Theta^{(L)} }\underbrace{\frac{a^{(L-1)} }{z^{(L-1)} } }_{g'(z^{(L-1)})}\underbrace{\frac{z^{(L-1)} }{\Theta^{(L-1)} } }_{a^{(L-2)} } \end{aligned} \]
这其中,一个个的导数都是可以计算出来的。因此我们就得到了最终的梯度: \[ \begin{aligned} \frac{\partial L}{a^{(L)} } \frac{a^{(L)} }{z^{(L)} } \frac{z^{(L)} }{a^{(L-1)} }\frac{a^{(L-1)} }{z^{(L-1)} }\frac{z^{(L-1)} }{\Theta^{(L-1)} } = \underbrace{(a^{(L)} - y)}_{s_L\times1}\underbrace{\Theta^{(L)} }_{s_l \times s_{l-1} }\underbrace{g'(z^{(L-1)})}_{s_{l-1} \times 1}\underbrace{a^{(L-2)} }_{s_{l-2} \times 1} \end{aligned} \]
不过需要注意的是,上面得到的导数你会发现矩阵的维度可能不合适。因此这个形式必须要重新组织一下: \[ \underbrace{\frac{\partial L}{\partial \Theta^{(L-1)} } }_{s_{l-1} \times s_{l-2} }=\underbrace{(\Theta^{(L)})^T }_{s_{l-1} \times s_{l} }\underbrace{(a^{(L)}-y)}_{s_l \times 1} .* \underbrace{g'(z^{(L-1)})}_{s_{l-1}\times 1}\underbrace{(a^{(L-2)})^T}_{1 \times s_{l-2} } \]
如果想要计算更前面的参数矩阵的导数,这个链式法则会越来越长。
为了更好的计算各个层的梯度,我们新定义一个符号: \[ \sigma^{(l)} = \nabla_{z^{(l)} }L(y,y') \]
- \(l = L\)
有时候我们可以直接计算出来\(\nabla_{z^{(L)} }L(y,y')\)(g为softmax函数),有时候需要使用链式法则:
\(\nabla_{z^{(L)} }L(y,y') = \nabla_{y'}L(y',y) .* g'(z^{(L)})\)
- \(l \ne L\)
\(\sigma^{l} = ((\Theta^{(l+1))^T}\sigma^{(l+1)}) .*g'(z^{(l)})\)
- \(\nabla _{\Theta^{(l)} } L = \sigma^{(l)}(a^{(l-1)})^T\)
通过验证你会发现实际上上面说的正是我们推导的内容。
使用梯度下降,或者SGD(更加常用),最终求得合适的\(\Theta\).
可以看到的\(\sigma^{(l)}\)的计算,需要的是后向计算,所以这个叫后向传播。
上面的推导过程都是以一个training example的,对于多个样本可以通过向量化以及矩阵化来加快实现。
参考文献: