机器学习——Kernel Support Vector Macine
上次遇到的问题是,Q矩阵的计算,仍然可能需要耗费很大计算量,也就是对于很高维度的特征转换,我们不一定能高效解决,更不用说无限维度。
因此这次引入了核函数,告诉我们如何高效地对待特征转换地问题。
Polynomial Kernel
为了方便起见,我们希望可以把原来问题描述中的\(X\)换为\(Z\),表示\(Z\)是\(X\)经过特征转换之后得到的高维度空间,而假设\(X\)维度是较低的。因此,现在的问题描述如下:
\(min_{\alpha} \frac 1 2 \sum_{n=1}^N \sum_{m=1}^N a_na_my_ny_mZ_n^TZ_m - \sum_{n=1}^N \alpha_n\)
subject to \(\sum_{n=1}^N y_n\alpha_n = 0;a_n \ge 0,n=1,...,N\)
上次我们也介绍了Q矩阵的计算,其中\(q_{n,m} = y_ny_mZ_n^TZ_m\).这其中包含了对\(Z\)向量的乘积,因此隐含了很大的计算量。
假设,我们对\(X\)到\(Z\)向量的转换表示如下:\(Z = \phi(X)\),那么上式中\(Z_n^TZ_m = \phi(X_n)^T\phi(X_m)\).
我们知道,对于单单\(X_n^TX_m\)的计算是容易完成的,那么能不能通过什么办法用上面的计算来代替原来的硬算?
假设如下:\(\phi(X) = {1,x_1,x_2,x_3...x_d,x_1^2,x_1x_2,...x_2x_1,x_2^2,...,x_dx_1,...x_d^2}\).
那么$(X_n)^T(X_m) = 1 + {i=1}{d}x_inx_i^m + {i=1}^d_{j=1}^d x_inx_jnx_imx_jm $
$(X_n)^T (X_m) = 1+X_n^TX_m + {i=1}{d}x_inx_i^m {j=1}^{d} x_j^n x_j^m = 1+X_n^TX_m + (X_nTX_m)2 $.
可以发现,通过这样的变换,我们很轻易地计算出\(Z_n^TZ_m\).
在这里,我们称$k(X,X') = 1+X^TX' + (XTX')2 \(为一种核函数。如果我们对特征转换再进行一些处理,比如:\)(X) = {1, x_1, x_2, x_3... x_d,x_12,x_1x_2,...x_2x_1,x_22,...,x_dx_1,...x_d^2}$,
那么最后得到的是\(k(x,x') = (1+X^TX')^2\)。实际上,我们也可以转换到更高维的空间,继续推广到更一般的:\(K(x,x') = (\zeta + \xi x^Tx')^d\). 这就是很有名的Polynomial Kernel。
当然,通过多项式核函数,我们无法实现无限维度的转换。
Gaussian Kernel(RBF Kernel)
对于高斯Kernel的介绍,我们尝试用另一种办法来推导。为了方便起见,我们假设维度只有一维,即\(X = {x}\).
在这里直接给出\(K(X,X')\)的定义如下:\(K(X,X') = e^{-(x -x')^2}\).
然后我们一步步推向前推导,说明它其实是无限维度转换后的\(X^TX\). \[ \begin{align} K(X,X') &= e^{-(x - x')^2}\\ &= e^{-x^2} e^{-(x')^2}e^{2xx'} \\ &=Taylor=>e^{-x^2}e^{-(x')^2}(\sum _{i=0} ^ {\infty} \frac {(2xx')^2}{i!})\\ &= \sum_{i=0}^{\infty} \frac {(\sqrt 2 x)^i}{\sqrt{i!} }e^{-x^2} \frac {(\sqrt 2 x')^i}{\sqrt{i!} } e^{-(x')^2} \end{align} \]
因此,这个转换就是 \(\phi(x) = exp(-x^2)(1,\sqrt{\frac 2 {1!} }X,\sqrt{\frac {2^2}{2!} }X^2,...)\)
可以证明的是,上升到多维度,Gaussian Kernel:
\(K(X,X')\) = \(e^{-\gamma ||X - X'||^2}\) with \(\gamma > 0\).
这就是高斯核函数。但是需要注意的一点,高斯核函数放大无限维度空间,所以如果参数\(\gamma\)不当,仍然有可能overfitting.如下图:
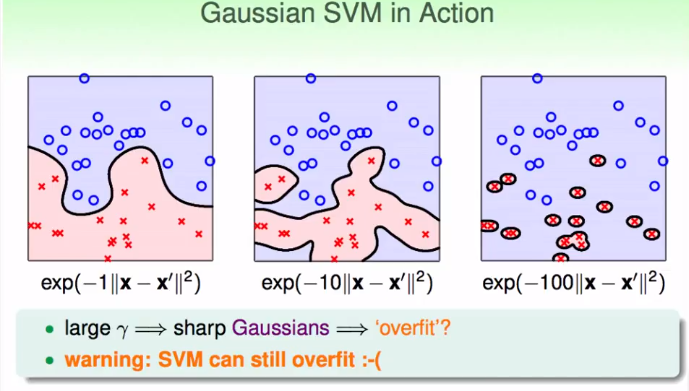
Comparison
还有一个核函数,叫线性核函数:\(K(x,x') = x^Tx'\).
这个核函数,简单,也迅速,但是能力有限。
多项式核函数:\(K(x,x') = (\zeta + \xi x^tx')^d\).
相对于线性核函数,它的能力强了很多,但是调参很难,因为有3个参数。相应的它的速度没有线性那么快。而且如果d很大,要么结果很接近0,要么很大,不会取得很好的结果。因此,它一般来说,只在d比较小的时候适用。
高斯核函数:\(K(X,X')\) = \(e^{-\gamma ||X - X'||^2}\)
高斯核函数很强大,计算速度比线性的略慢,但是也不差。但是它可能太过强大了,需要慎重适用,因为可能出现过拟合的情况。但是总体来说,一般来说高斯核函数是最常用的。
当然,还有很多别的核函数,只需要满足Mercer定理即可。
Mercer定理:
如果函数K是\(\mathcal{R}^n \times \mathcal{R}^n->\mathcal{R}\)上的映射(也就是从两个n维向量映射到实数域)。那么如果K是一个有效核函数(也称为Mercer核函数),那么当且仅当对于训练样例\({x_1,x_2,...x_n}\),其相应的核函数矩阵是对称半正定的。
我们可以发现,kernel的区别实际上是特征转换的区别,只不过某些特征转换可以更容易地计算Q矩阵。