机器学习——Linear Support Vector Machine

Posted on 2018-10-10 Edited on 2018-11-02 In 机器学习

这个名字真是很奇怪。想要了解为何叫这么奇怪的名字，就要深入了解这个东西。首先需要回顾的是之前的Perceptron Learning Algorithm。如果这个资料线性可分，使用PLA算法，一定可以找到一个很好的线或者超平面（hyperplane）来将这个资料分开，但是这个线或者是超平面的个数可能是无数个，它们是否是一样好的？如下图：

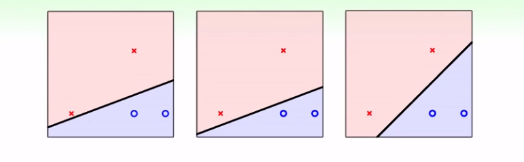
上面3条线，对于PLA算法来说是一样好的，因此运行到哪一条，都是无法预测的。但是从我们的角度来看，我们会选择第三条，因为这条线更robust，可以容忍更多测量误差，如第一条，有一个离红色点很近的样本的话，它更大概率是negative的，但是第一条就会将它归类到positive。因此，选择第三条线，可以更好地避免overfitting。

为了想解决这个问题，我们需要将问题提炼成数学语言。首先我们想要求的是灰色区域最大的：

我们称灰色区域为margin。而这个margin，实际上是最近的两个点到中间这条线的距离。

那么我们就要先想象，点到平面（或者超平面）的距离如何计算？

如果一个超平面的方程为$W^TX + b = 0$,则任意两个在该平面的点$x'$与$x''$都应该满足上式，也就是 \[ \left\{ \begin{array} W^TX'+b = 0\\ W^TX''+b = 0 \end{array} \right \] 因此可以得到：$W^T(X'-X'') = 0$. 而$(X'-X'')$可以表示平面上的任何一个向量，这说明了，$W$是该平面的法向量。

而一个点到平面的距离，实际上就是该点到任何平面上一点连接得到的向量对该平面法向量的一个投影。计算投影长度的办法其实很简单,首先我们有$ab = |a||b|cos\theta$,因此只要规定a的长度为1，那么这两个向量的数量积的绝对值就是向量的长度。因此我们可以得到： \[ d = |\frac {W^T }{||W||}(X - X')| = |\frac 1 {||W||}(W^TX + b)|. \]

这样，我们就得到了一个点到一个超平面的距离。

实际上一个超平面的表示方法是无穷的，比如$WTX+b = 0$与$2W^TX+2b= 0$是一个平面，如果我们将经过距离超平面最近的点的与超平面平行的平面表示为:$W^X+b = ±1$，那么d的形式就更简单了：$d = \frac 1 {||W||}$.

上面的距离中还是加了绝对值，但是因为这个问题的前提是将所有的点都分类正确，因此$y_i(WX_i+b)\ge 0$.

所以用数学语言描述我们的问题如下：

max $\frac 1 {||W||}$

$s.t. min_{n = 1,...,N} y_n(W^TX_n+b) = 1$.

注意的是为什么最小的点$y_n(W^TX_n+b) = 1$,因为距离较远的话，根据距离公式$(W^TX+b)$会更大。

上面的问题依然是很难解决的，我们希望可以继续放松这个约束。如果是所有点$y_n(W^TX_n+b) \ge 1$如何呢？

这里利用反证法证明，放宽到上面的约束依然没有问题，距离直线最近的点依然是满足$y_n(W^TX_n+b) = 1$：

如果我们找到最近的点$X_n$，它满足的是$y_n(W^TX_n+b) =a (a>1)$，而且得到了最大的$\frac 1 {||W||}$，那么对上式左右同时除以a,而$\frac W a$比$W$更小，也就是这个$\frac 1 {||W||}$并不是最大的。这就矛盾了。因此依然只有在$y_n(W^TX_n+b) =1$的时候才能取得最大值。所以放大这个约束，我们依然可以得到一样的最终结果。

之前我们一直在求得是最小值，我们希望在这里也可以转换成为求最小值，同时范数是需要根号的，而因为范数和范数的平方是单调递增的，因此转化为范数的平方不会影响结果，同时再添上一个$\frac 1 2$，为了以后计算的方便。

因此，最终的用数学语言描述我们的问题的版本如下：

min $\frac 1 2W^TW$

$s.t. y_n(W^TX_n+b) ,n =1,2,...,N $.

这个问题实际上是一个QP（二次规划）问题。而二次规划问题，我们可以借助很多工具，提供必要的参数，求得最佳解。

上术问题就是svm问题。为什么叫support vector machine？我们需要注意的是，实际上决定最终线的，只有可能是最边上的点，而决定最终结果的点，就叫做支持向量。

当我们面对线性无法可分的情况，就需要使用之前介绍的特征转换（nonlinear transform），将当前的点转换到更高维度的空间中去，使其成为线性可分。

最后，我们在这里想要简单说明一下这背后的理论基础，为什么寻找最粗的那条线，可以获得更好的robustness？

这就又回到了vc dimension.假设我们找到的比较粗的线（margin较大），是我们要的标准。那么具有这么大margin的线，能将空间中的N个样本分成的dichotomy的个数就会少很多，也就是有效vc dimension会变低。当然，这个问题无法像PLA时候那样分析，因为具体能分多少，与样本之间的距离也很重要，具体样本得到的结果也不同，但是可以证明的是,如果这些样本在一个半径为R的圆内，margin长度为ρ：

\[ d_{vc}(\mathcal{A}_{\rho}) \leq min(\frac {R^2}{ρ^2} ,d)+1 \leq d+1 \]

之前介绍的feature transform有个问题是太过于复杂导致vc dimension会变得很大，而我们可以看出来通过SVM我们某种程度上可以处理好这种情况。